题目内容
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为函数f(x)的不动点;已知f(x)=x2+bx+c.
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)已知当c= 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围?
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)已知当c=
 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围?解:(1)∵f(x)有两个不动点为﹣3,2,
∴﹣3,2是方程x2+bx+c=x的两根,
整理得:x2+(b﹣1)x+c=0,
∴﹣3+2=1﹣b,﹣3×2=c,
∴b=2,c=﹣6.
∴f(x)=x2+bx+c=x2+2x﹣6
由f(x)=0得其零点为x1,2=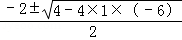 =﹣1±
=﹣1±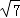 .
.
(2)∵c=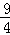 时,函数f(x)没有不动点,
时,函数f(x)没有不动点,
∴x2+(b﹣1)x+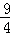 =0无实数根,
=0无实数根,
∴△=(b﹣1)2﹣9<0,
解得﹣2<b<4.
∴实数b的取值范围为:﹣2<b<4.
∴﹣3,2是方程x2+bx+c=x的两根,
整理得:x2+(b﹣1)x+c=0,
∴﹣3+2=1﹣b,﹣3×2=c,
∴b=2,c=﹣6.
∴f(x)=x2+bx+c=x2+2x﹣6
由f(x)=0得其零点为x1,2=
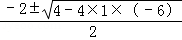 =﹣1±
=﹣1±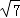 .
.(2)∵c=
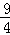 时,函数f(x)没有不动点,
时,函数f(x)没有不动点,∴x2+(b﹣1)x+
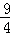 =0无实数根,
=0无实数根,∴△=(b﹣1)2﹣9<0,
解得﹣2<b<4.
∴实数b的取值范围为:﹣2<b<4.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目