题目内容
已知椭圆的一个焦点F1(0,-2
),且离心率e满足
,e,
成等比数列.
(1)求椭圆的标准方程;
(2)试问是否存在直线l,使l与椭圆交于不同的两点M,N,且线段MN恰被点P(-
,
)平分.
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
(1)求椭圆的标准方程;
(2)试问是否存在直线l,使l与椭圆交于不同的两点M,N,且线段MN恰被点P(-
| 1 |
| 2 |
| 3 |
| 2 |
分析:(1)利用椭圆的一个焦点F1(0,-2
),且离心率e满足
,e,
成等比数列,求出几何量,从而可得椭圆的标准方程;
(2)利用点差法,结合线段MN恰被点P(-
,
)平分,可得直线方程,再进行验证,即可得到结论.
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
(2)利用点差法,结合线段MN恰被点P(-
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)e2=
,∴
=
,∵c=2
,∴a=3…(2分)
∴b2=1,∴
+x2=1…(4分)
(2)假设存在这样的直线l,设M(x1,y1),N(x2,y2)
则
+
=1,
+
=1,作差得(y1+y2)(y1-y2)+9(x1+x2)(x1-x2)=0…(6分)
∵线段MN恰被点P(-
,
)平分
∴x1+x2=-1,y1+y2=3
设直线l的斜率为k,则k=3,∴直线l的方程为y=3x+3…(10分)
检验:
,整理得x2+x=0显然△>0
检验成立,所以存在这样的直线l….(12分)
| 8 |
| 9 |
| c |
| a |
2
| ||
| 3 |
| 2 |
∴b2=1,∴
| y2 |
| 9 |
(2)假设存在这样的直线l,设M(x1,y1),N(x2,y2)
则
| ||
| 9 |
| x | 2 1 |
| ||
| 9 |
| x | 2 2 |
∵线段MN恰被点P(-
| 1 |
| 2 |
| 3 |
| 2 |
∴x1+x2=-1,y1+y2=3
设直线l的斜率为k,则k=3,∴直线l的方程为y=3x+3…(10分)
检验:
|
检验成立,所以存在这样的直线l….(12分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
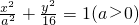 的一个焦点F(3,0),则a=________.
的一个焦点F(3,0),则a=________. 的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F,
,倾斜角为45°的直线l过点F, 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= . 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= .