题目内容
6.已知指数函数f(x)=ax(a>0,且a≠1)的图象过点(-2,$\frac{9}{4}$).(1)求函数的解析式:
(2)求f(0),f(1),f(-3),f(-$\frac{1}{2}$):
(3)作出函数的图象:
(4)指出函数的单调区间和奇偶性:
分析 (1)由于指数函数f(x)=ax(a>0,且a≠1)的图象过点(-2,$\frac{9}{4}$),代入可得$\frac{9}{4}={a}^{-2}$,解得a.即可得出f(x)
(2)代入f(x)即可得出.
(3)如图所示,
(4)利用指数函数的单调性与奇偶性即可得出.
解答 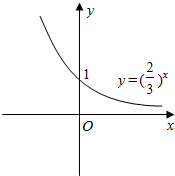 解:(1)∵指数函数f(x)=ax(a>0,且a≠1)的图象过点(-2,$\frac{9}{4}$),
解:(1)∵指数函数f(x)=ax(a>0,且a≠1)的图象过点(-2,$\frac{9}{4}$),
∴$\frac{9}{4}={a}^{-2}$,解得a=$\frac{2}{3}$.
∴f(x)=$(\frac{2}{3})^{x}$.
(2)f(0)=1,f(1)=$\frac{2}{3}$,f(-3)=$\frac{27}{8}$,$f(-\frac{1}{2})$=$\frac{\sqrt{6}}{2}$.
(3)如图所示,
(4)函数f(x)在R上单调递减,非奇非偶函数.
点评 本题考查了指数函数的图象与性质,考查了数形结合方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知α为第三象限角,则tan$\frac{α}{2}$的值( )
| A. | 一定为正数 | B. | 一定为负数 | ||
| C. | 可能为正数,也可能为负数 | D. | 不存在 |
18.若关于x的方程(log2x)2+2alog2x+1=0有大于1的实数解,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | (1,+∞) | D. | (-∞,-1]∪[1,+∞) |
15.不等式2+log0.5(5-x)+log2$\frac{1}{x}$>0的解集是( )
| A. | (0,+∞) | B. | (-∞,5) | C. | (0,1)∪(4,5) | D. | 空集 |