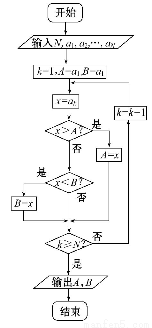
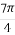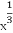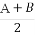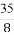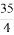题目内容
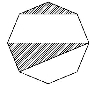
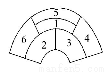
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).
120
【解析】方法一:从题意来看,6部分种4种颜色的花,又从图形看,知必有2组同颜色的花,从同颜色的花入手分类求解.
(1)2与5同色,则3,6也同色或4,6也同色,所以共有N1=4×3×2×2×1=48(种);
(2)3与5同色,则2,4或4,6同色,所以共有N2=4×3×2×2×1=48(种);
(3)2与4且3与6同色,所以共有N3=4×3×2×1=24(种).
所以,共有N=N1+N2+N3=48+48+24=120(种).
方法二:记颜色为A,B,C,D四色,先安排1,2,3有4×3×2种不同的栽法,不妨设1,2,3已分别栽种A,B,C,则4,5,6栽种方法共5种,由以下树状图清晰可见.

根据分步乘法计数原理,不同的栽种方法有N=4×3×2×5=120(种).

练习册系列答案
相关题目
若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
分 组 | 频 数 | 频 率 |
[-3,-2) |
| 0.10 |
[-2,-1) | 8 |
|
(1,2] |
| 0.50 |
(2,3] | 10 |
|
(3,4] |
|
|
合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填充完整.
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率.
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.