题目内容
已知 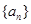 是等差数列,
是等差数列,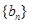 是公比为
是公比为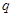 的等比数列,
的等比数列,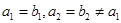 ,记
,记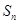 为数列
为数列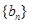 的前
的前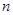 项和,
项和,
(1)若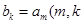 是大于
是大于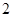 的正整数
的正整数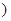 ,求证:
,求证: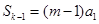 ;
;
(2)若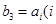 是某一正整数
是某一正整数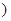 ,求证:
,求证: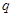 是整数,且数列
是整数,且数列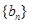 中每一项都是数列
中每一项都是数列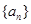 中的项;
中的项;
(3)是否存在这样的正数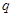 ,使等比数列
,使等比数列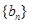 中有三项成等差数列?若存在,写出一个
中有三项成等差数列?若存在,写出一个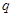 的值,并加以说明;若不存在,请说明理由;
的值,并加以说明;若不存在,请说明理由;
【答案】
(1)
(2)存在 使得
使得 中有三项
中有三项 成等差数列。
成等差数列。
【解析】
试题分析:设 的公差为
的公差为 ,由
,由 ,知
,知 ,
, (
( )
)
(1)因为 ,所以
,所以 ,
,
 ,
,
所以
(2) ,由
,由 ,
,
所以 解得,
解得, 或
或 ,但
,但 ,所以
,所以 ,因为
,因为 是正整数,所以
是正整数,所以 是整数,即
是整数,即 是整数,设数列
是整数,设数列 中任意一项为
中任意一项为
 ,设数列
,设数列 中的某一项
中的某一项
 =
=
现在只要证明存在正整数 ,使得
,使得 ,即在方程
,即在方程 中
中 有正整数解即可,
有正整数解即可, ,所以
,所以
 ,若
,若 ,则
,则 ,那么
,那么 ,当
,当 时,因为
时,因为 ,只要考虑
,只要考虑 的情况,因为
的情况,因为 ,所以
,所以 ,因此
,因此 是正整数,所以
是正整数,所以 是正整数,因此数列
是正整数,因此数列 中任意一项为
中任意一项为
 与数列
与数列 的第
的第 项相等,从而结论成立。
项相等,从而结论成立。
(3)设数列 中有三项
中有三项 成等差数列,则有
成等差数列,则有
2 设
设 ,所以2
,所以2 ,令
,令 ,则
,则
 ,因为
,因为 ,所以
,所以 ,所以
,所以 ,即存在
,即存在 使得
使得 中有三项
中有三项 成等差数列。
成等差数列。
考点:本题主要考查等比数列的通项公式、求和公式,等差数列的概念。
点评:难题,等比数列、等差数列相关内容,已是高考必考内容,其难度飘忽不定,有时突出考查求和问题,如“分组求和法”、“裂项相消法”、“错位相减法”等,有时则突出涉及数列的证明题,如本题,突出考查学生的逻辑思维能力。本题解法中,注意通过构造“一般项”加以研究,带有普遍性。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明. 至多有一个元素;
至多有一个元素; .
. 是等差数列,
是等差数列, 是其前
是其前 项和,
项和, ,则过点
,则过点 的直线的斜率是( )
的直线的斜率是( ) C.
C. D.
D.
 是等差数列,
是等差数列, 是各项为正数的等比数列,且
是各项为正数的等比数列,且 ,
, ,
, .
.  ,求数列
,求数列 的前
的前 项和
项和 .
. 是等差数列,
是等差数列, 是其前n项和,
是其前n项和, ,
, ,则过点P(3,
,则过点P(3, ),Q(4,
),Q(4, )的直线的斜率是
)的直线的斜率是 C.-4 D.-14
C.-4 D.-14