题目内容
已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若4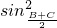 -cos2A=
-cos2A= ,b+c=
,b+c= ,求A、B、C的大小.
,求A、B、C的大小.
解:∵4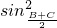 -cos2A=
-cos2A= ,
,
即4 -(2cos2A-1)=
-(2cos2A-1)= ,
,
∴2+2cosA-2cos2A+1= ,
,
即2cos2A-2cosA+ =0
=0
解得cosA=
∵A∈(0,π)
∴A=
又b+c= ,由正弦定理得:sinB+sinC=
,由正弦定理得:sinB+sinC= sinA=
sinA=
∴sin( -C)+sinC=
-C)+sinC=
∴sin(C+ )=
)=
∴C+ =
= ,或C+
,或C+ =
=
∴C= ,或C=
,或C=
∴A= ,B=
,B= ,C=
,C= ,或A=
,或A= ,B=
,B= ,C=
,C=
分析:由已知中4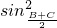 -cos2A=
-cos2A= ,我们可以根据同角三角函数关系及二倍角公式,我们可以构造关于A的三角方程,解方程即可求出A,由b+c=
,我们可以根据同角三角函数关系及二倍角公式,我们可以构造关于A的三角方程,解方程即可求出A,由b+c= ,利用正弦定理,我们进一步可以求出B,C值,得到答案.
,利用正弦定理,我们进一步可以求出B,C值,得到答案.
点评:本题考查的知识点是正弦定理,同角三角函数关系,二倍角公式,其中根据已知条件构造满足条件的三角方程是解答本题的关键.
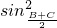 -cos2A=
-cos2A= ,
,即4
 -(2cos2A-1)=
-(2cos2A-1)= ,
,∴2+2cosA-2cos2A+1=
 ,
,即2cos2A-2cosA+
 =0
=0解得cosA=

∵A∈(0,π)
∴A=

又b+c=
 ,由正弦定理得:sinB+sinC=
,由正弦定理得:sinB+sinC= sinA=
sinA=
∴sin(
 -C)+sinC=
-C)+sinC=
∴sin(C+
 )=
)=
∴C+
 =
= ,或C+
,或C+ =
=
∴C=
 ,或C=
,或C=
∴A=
 ,B=
,B= ,C=
,C= ,或A=
,或A= ,B=
,B= ,C=
,C=
分析:由已知中4
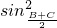 -cos2A=
-cos2A= ,我们可以根据同角三角函数关系及二倍角公式,我们可以构造关于A的三角方程,解方程即可求出A,由b+c=
,我们可以根据同角三角函数关系及二倍角公式,我们可以构造关于A的三角方程,解方程即可求出A,由b+c= ,利用正弦定理,我们进一步可以求出B,C值,得到答案.
,利用正弦定理,我们进一步可以求出B,C值,得到答案.点评:本题考查的知识点是正弦定理,同角三角函数关系,二倍角公式,其中根据已知条件构造满足条件的三角方程是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目