题目内容
已知正六棱锥P-ABCDEF的底面边长为1cm,侧面积为3cm2,则该棱锥的体积为______cm3.
S-ABCDEF为正六棱锥,O是底面正六边形ABCDEF的中心.
连接OA、OB、OS,过O作边AB的垂线,垂足为Q.则:
因为ABCDEF为正六边形,所以:△AOB为等边三角形.
所以:OA=OB=AB=1,又因为OQ⊥AB,所以:Q是AB中点
所以,AQ=BQ=
因为OP⊥面ABCDEF,所以:OP⊥OQ,
所以,△OPQ为直角三角形.在Rt△OPQ中,
×AB×PQ=
,
∴斜高PQ=1,
在直角三角形POQ中,高PO=
=
=
,
则该棱锥的体积为V=
×6×
×
=
cm3
故答案为:
.
连接OA、OB、OS,过O作边AB的垂线,垂足为Q.则:
因为ABCDEF为正六边形,所以:△AOB为等边三角形.
所以:OA=OB=AB=1,又因为OQ⊥AB,所以:Q是AB中点
所以,AQ=BQ=
| 1 |
| 2 |
因为OP⊥面ABCDEF,所以:OP⊥OQ,
所以,△OPQ为直角三角形.在Rt△OPQ中,
| 1 |
| 2 |
| 3 |
| 6 |
∴斜高PQ=1,
在直角三角形POQ中,高PO=
| PQ2-OQ2 |
12-(
|
| 1 |
| 2 |
则该棱锥的体积为V=
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
故答案为:
| ||
| 4 |

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目


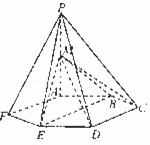
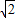 ,M是PA的中点.
,M是PA的中点.
 ,M是PA的中点.
,M是PA的中点.