题目内容

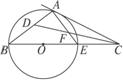
如图2-4-13,BA是⊙O的直径,AD是⊙O的切线,切点为A,BF、BD交AD于点F、D,交⊙O于E、C,连结CE.求证:BE·BF =BC·BD.

图2-4-13

思路分析:要证BE·BF =BC·BD,只需证△BEC∽△BDF,∠DBF为公共角,只需再找一组角相等,为此,过B作⊙O的切线,构造弦切角.

证明:过B作⊙O的切线BG,则BG∥AD,?

∴∠GBC =∠BDF.?

又∵∠GBC =∠BEC,?

∴∠BEC =∠BDF.?

而∠CBE为公共角,?

∴△BEC∽△BDF.?

∴BE·BF =BC·BD.

练习册系列答案
相关题目
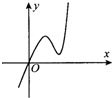精英家教网定义在R上的函数f（x）满足f（4）=1．f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若两正数a，b满足f（2a+b）＜1，则
b+2
a+2
的取值范围是（　　）
A、(
1
3
，
1
2
)
B、(-∞，
1
2
)∪(3，+∞)
C、(
1
2
，3)
D、（-∞，-3）
如图2-13,⊙O中弦AB、CD相交于点F,AB=10,AF=2,若CF∶DF=1∶4,则CF的长为(    )

图2-13

A.               B.2                 C.3                D.

如图2-4,已知Rt△ABC中,∠B=90°,AC=13,AB=5,O是AB上的点,以O为圆心,OB为半径作⊙O.

(1)当OB=2.5时,⊙O交AC于点D,求CD的长.

(2)当OB=2.4时,AC与⊙O的位置关系如何?试证明你的结论.

图2-4

如图2-2-13，在ABCD中，设=a，=b.

则(1)当a、b满足什么条件时，a+b与a-b垂直?

(2)当a、b满足什么条件时，|a+b|=|a-b|?

(3)a+b与a-b可能是相等向量吗?

(4)当a与b满足什么条件时，a+b平分a与b所夹的角?

图2-2-13

如图2-4-13，已知C点在⊙O直径BE的延长线上，CA切⊙O于A点，∠ACB的平分线CD交AE于F点，交AB于D点.

图2-4-13

(1)求∠ADF的度数.

(2)若∠ACB的度数为y度，∠B的度数为x度，那么y与x之间有怎样的关系？试写出你的猜测并给出证明.

(3)若AB=AC，求AC∶BC.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网