题目内容
在如图所示的多面体中，已知正三棱柱ABC﹣A1B1C1的所有棱长均为2，
四边形ABCD是菱形．
（Ⅰ）求证：平面ADC1⊥平面BCC1B1；
（Ⅱ）求该多面体的体积．
四边形ABCD是菱形．
（Ⅰ）求证：平面ADC1⊥平面BCC1B1；
（Ⅱ）求该多面体的体积．
（Ⅰ）∵三棱柱ABC﹣A1B1C1是正三棱柱，
∴BB1⊥AD，
又∵四边形ABDC是菱形，
∴AD⊥BC，
∵BB1，BC
平面BB1C1C，且BC∩BB1=B，
∴AD⊥平面BCC1B1
∵AD
平面ADC1，
∴平面ADC1⊥平面BCC1B1
（Ⅱ）∵正三角形ABC边长为2，可得S△ABC=
×22=
，三棱柱的高AA1=2
∴正三棱柱ABC﹣A1B1C1的体积为
又∵AD⊥平面BCC1B1，可得四棱锥D﹣B1C1CB的高在AD上且等于AD的
∴四棱锥D﹣B1C1CB的体积为
所以该多面体的体积为
∴BB1⊥AD，
又∵四边形ABDC是菱形，
∴AD⊥BC，
∵BB1，BC
平面BB1C1C，且BC∩BB1=B，∴AD⊥平面BCC1B1
∵AD
平面ADC1，∴平面ADC1⊥平面BCC1B1
（Ⅱ）∵正三角形ABC边长为2，可得S△ABC=
×22=，三棱柱的高AA1=2∴正三棱柱ABC﹣A1B1C1的体积为
又∵AD⊥平面BCC1B1，可得四棱锥D﹣B1C1CB的高在AD上且等于AD的
∴四棱锥D﹣B1C1CB的体积为
所以该多面体的体积为
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
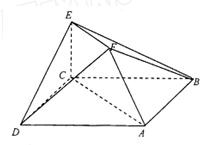在如图所示的多面体中，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EC⊥AC，EF∥AC，AB=
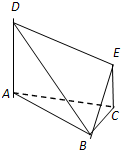在如图所示的多面体中，底面△ABC是边长为2的正三角形，DA和EC均垂直于平面ABC，且DA=2，EC=1．
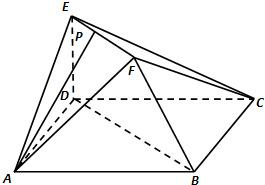在如图所示的多面体中，已知正方形ABCD和
（2012•日照一模）在如图所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC=2AD=4，EF=3，AE=BE=2，G是BC的中点．
在如图所示的多面体中，AA1∥BB1，CC1⊥AC，CC1⊥BC．