题目内容
已知f(x)=x2-2x+3,g(x)=x2-1,讨论f[g(x)]的单调性与奇偶性,并画出它的草图.
解:f[g(x)]=[g(x)]2-2[g(x)]+3
=(x2-1)2-2(x2-1)+3
=x4-4x2+6.
显然f[g(x)]是偶函数.
|f[g(x)]|x′=4x3-8x.
令4x3-8x>0,解得-![]() <x<0,或x>
<x<0,或x>![]() .
.
令4x3-8x<0,解得x<-![]() ,或0<x<
,或0<x<![]() .
.
所以复合函数f[g(x)]的增区间是(-![]() ,0)与(
,0)与(![]() ,+∞),减区间是(-∞,-
,+∞),减区间是(-∞,-![]() )与(0,
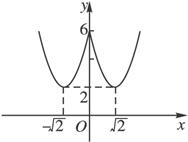
)与(0,![]() ).它的图象如图.
).它的图象如图.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目