题目内容
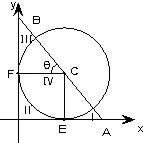过圆C：（x-1）2+（y-1）2=1的圆心，作直线分别交x、y正半轴于点A、B，△AOB被圆分成四部分（如图），若这四部分图形面积满足S|+SIV=S||+S|||则直线AB有（ ）| A、0条 | B、1条 | C、2条 | D、3条 |
分析：由圆的方程得到圆心坐标和半径，根据四部分图形面积满足S|+SIV=S||+S|||，得到SIV-SII=SⅢ-SI，第II，IV部分的面积是定值，所以三角形FCB减去三角形ACE的面积为定值即SⅢ-SI为定值，所以得到满足此条件的直线有且仅有一条，得到正确答案．
解答：解：由已知，得：SIV-SII=SⅢ-SI，
由图形可知第II，IV部分的面积分别为S正方形OECF-S扇形ECF=1-
和S扇形ECF=
，
所以，SIV-SII为定值，即SⅢ-SI为定值，
当直线AB绕着圆心C移动时，
只可能有一个位置符合题意，即直线AB只有一条．
故选B．
由图形可知第II，IV部分的面积分别为S正方形OECF-S扇形ECF=1-
| π |
| 4 |
| π |
| 4 |
所以，SIV-SII为定值，即SⅢ-SI为定值，
当直线AB绕着圆心C移动时，
只可能有一个位置符合题意，即直线AB只有一条．
故选B．
点评：此题考查学生掌握直线与圆的位置关系，会求三角形、正方形及扇形的面积，是一道综合题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
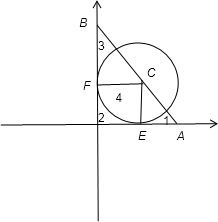过圆C：（x-1）2+（y-1）2=1的圆心，作直线分别交x、y正半轴于点A、B，△AOB被圆分成四部分（如图），若这四部分图形面积满足S1+S4=S2+S3则直线AB有
过圆C：（x-1）2+（y-1）2=1的圆心，作直线分别交x，y正半轴于点A、B，△AOB被圆分成I、II、III、IV四个部分（如图），若这四部分图形面积满足①SI+SIV=SII+SIII，②SI+SII+SIII=SIV，则分别满足①、②的直线AB各有（ ）
