题目内容
函数f(x)=x(x-m)满足f(
+x)=f(
-x),且在区间[a,b]上的值域是[-1,3],则点(a,b)的轨迹是图中的( )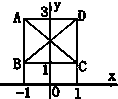
| 1 |
| 2 |
| 3 |
| 2 |

| A、线段AB和线段AD |
| B、线段AB和线段CD |
| C、线段AD和线段BC |
| D、线段AC和线段BD |
分析:由函数满足f(
+x)=f(
-x)可得函数关于x=1对称,从而可得,f(x)=x(x-2)=(x-1)2-1,要使得函数的值域为[-1,3],则函数的定义域内必须有x=1,且x不能超过3,-1,结合二次函数的图象可得当a=-1时,1≤b≤3,当b=3时,1-≤a≤1,从而可求
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:由函数满足f(
+x)=f(
-x)可得函数关于x=1对称
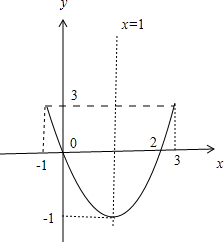
f(x)=x(x-m)的对称轴为x=1,从而有m=2,f(x)=x(x-2)=(x-1)2-1
由二次函数的性质可知,要使得函数的值域为[-1,3],则函数的定义域内必须有x=1,且x不能超过3,-1
所以,当a=-1时,1≤b≤3,则点(a,b)所表示的轨迹为线段AB
当b=3时,1-≤a≤1,则点(a,b)所表示的轨迹为线段AD
故选:A
| 1 |
| 2 |
| 3 |
| 2 |
f(x)=x(x-m)的对称轴为x=1,从而有m=2,f(x)=x(x-2)=(x-1)2-1
由二次函数的性质可知,要使得函数的值域为[-1,3],则函数的定义域内必须有x=1,且x不能超过3,-1
所以,当a=-1时,1≤b≤3,则点(a,b)所表示的轨迹为线段AB
当b=3时,1-≤a≤1,则点(a,b)所表示的轨迹为线段AD
故选:A

点评:本题主要考查了二次函数的性质(对称性、函数的定义域域函数的值域)的应用,解题的关键是熟练应用二次函数的图象.

练习册系列答案
相关题目
探究函数f(x)=x+
x∈(0,+∞)的最小值,并确定相应的x的值,列表如下,请观察表中y值随x值变化的特点,完成下列问题:
(1)若当x>0时,函数f(x)=x+
时,在区间(0,2)上递减,则在 上递增;
(2)当x= 时,f(x)=x+
,x>0的最小值为 ;
(3)试用定义证明f(x)=x+
,x>0在区间上(0,2)递减;
(4)函数f(x)=x+
,x<0有最值吗?是最大值还是最小值?此时x为何值?
解题说明:(1)(2)两题的结果直接填写在答题卷中横线上;(4)题直接回答,不需证明.
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
(2)当x=
| 4 |
| x |
(3)试用定义证明f(x)=x+
| 4 |
| x |
(4)函数f(x)=x+
| 4 |
| x |
解题说明:(1)(2)两题的结果直接填写在答题卷中横线上;(4)题直接回答,不需证明.