题目内容
已知抛物线y2=4x上一点，A（x0，y0），F是其焦点，若y0∈[1，2]，则|AF|的范围是
- A.
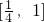
- B.
- C.[1，2]
- D.[2，3]
B
分析：根据抛物线的定义可知|AF|=x0+1，再根据y0的范围确定x0的范围，进而求得|AF|的范围．
解答：抛物线y2=4x，p=2，准线方程为x=-1
根据抛物线的定义可知，|AF|=x0+1
∵y0∈[1，2]，
∴
≤x0≤1
∴|AF|∈
故选B
点评：本题主要考查了抛物线的性质．属基础题．
分析：根据抛物线的定义可知|AF|=x0+1，再根据y0的范围确定x0的范围，进而求得|AF|的范围．
解答：抛物线y2=4x，p=2，准线方程为x=-1
根据抛物线的定义可知，|AF|=x0+1
∵y0∈[1，2]，
∴
≤x0≤1∴|AF|∈
故选B
点评：本题主要考查了抛物线的性质．属基础题．
练习册系列答案
名题金卷系列答案
相关题目
已知抛物线y2=4x，焦点为F，顶点为O，点P（m，n）在抛物线上移动，Q是OP的中点，M是FQ的中点．