题目内容
已知双曲线 经过点
经过点 ,其渐近线方程为y=±2x.
,其渐近线方程为y=±2x.(1)求双曲线的方程;
(2)设F1,F2是双曲线的两个焦点,证明:AF1⊥AF2.
【答案】分析:(1)根据题意,双曲线C的一条渐近线方程为 y=±2x,将点C坐标代入方程,列出关于a,b的方程,解出a,b,进而可得答案.
(2)由(1)得, ,
, ,从而以F1F2为直径的圆的方程,再根据点
,从而以F1F2为直径的圆的方程,再根据点 的坐标满足方程x2+y2=5,得出点A在以F1F2为直径的圆上,最终得出AF1⊥AF2.
的坐标满足方程x2+y2=5,得出点A在以F1F2为直径的圆上,最终得出AF1⊥AF2.
解答:(1)解:依题意 …(3分)
…(3分)
解得 …(5分)
…(5分)
所以双曲线的方程为 .…(6分)
.…(6分)
(2)由(1)得, ,
, ,
,
从而以F1F2为直径的圆的方程是x2+y2=5.…(9分)
因为点 的坐标满足方程x2+y2=5,
的坐标满足方程x2+y2=5,
故点A在以F1F2为直径的圆上,所以AF1⊥AF2.…(12分)
点评:本题考查双曲线的方程、双曲线的简单性质,涉及双曲线的方程与其渐近线的方程之间的关系,要求学生熟练掌握,注意题意要求是标准方程,答案必须写成标准方程的形式.
(2)由(1)得,
 ,
, ,从而以F1F2为直径的圆的方程,再根据点
,从而以F1F2为直径的圆的方程,再根据点 的坐标满足方程x2+y2=5,得出点A在以F1F2为直径的圆上,最终得出AF1⊥AF2.
的坐标满足方程x2+y2=5,得出点A在以F1F2为直径的圆上,最终得出AF1⊥AF2.解答:(1)解:依题意
 …(3分)
…(3分) 解得
 …(5分)
…(5分)所以双曲线的方程为
 .…(6分)
.…(6分)(2)由(1)得,
 ,
, ,
,从而以F1F2为直径的圆的方程是x2+y2=5.…(9分)
因为点
 的坐标满足方程x2+y2=5,
的坐标满足方程x2+y2=5,故点A在以F1F2为直径的圆上,所以AF1⊥AF2.…(12分)
点评:本题考查双曲线的方程、双曲线的简单性质,涉及双曲线的方程与其渐近线的方程之间的关系,要求学生熟练掌握,注意题意要求是标准方程,答案必须写成标准方程的形式.

练习册系列答案
相关题目
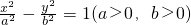 经过点
经过点 ,其渐近线方程为y=±2x.
,其渐近线方程为y=±2x. 经过点
经过点 ,其渐近线方程为y=±2x,
,其渐近线方程为y=±2x, 经过点
经过点 ,其渐近线方程为y=±2x.
,其渐近线方程为y=±2x.