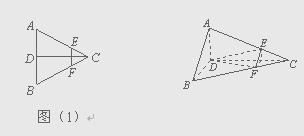题目内容
已知:a、b是异面直线,a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() ,a∥
,a∥![]() ,b∥
,b∥![]() .
.
![]() 求证:
求证: ![]() ∥
∥![]() .
.
证![]() 法1:在a上任取点P,
法1:在a上任取点P,
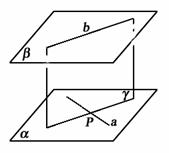 显然点P不在直线b上.
显然点P不在直线b上.![]() 于是b和点P确定平面
于是b和点P确定平面![]() ?.
?.
且![]() 与
与![]() 有公共点P ∴
有公共点P ∴ ![]() ∩
∩![]() =b′且b′和a交于P,
=b′且b′和a交于P,
∵ b∥![]() , ∴ b∥b′ ∴ b′∥
, ∴ b∥b′ ∴ b′∥![]() , 而a∥
, 而a∥![]() ?
?
这样![]() 内相交直线a和b′都平行于
内相交直线a和b′都平行于![]() ?
?
∴ ![]() ∥
∥![]() .
.
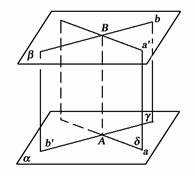 证法2:设AB是a、b的公垂线段,过AB和b作平面
证法2:设AB是a、b的公垂线段,过AB和b作平面![]() ,
,
则![]() ∩
∩![]() =b′,过AB和a作平面
=b′,过AB和a作平面![]() ,则
,则![]() ∩
∩![]() =a′.
=a′.
a∥![]()
![]() a∥a′ b∥
a∥a′ b∥![]()
![]() b∥b′
b∥b′
∴AB⊥a![]() AB⊥a′,AB⊥b
AB⊥a′,AB⊥b![]() AB⊥b′
AB⊥b′
于是AB⊥![]() ??且AB⊥
??且AB⊥![]() ?,∴
?,∴ ![]() ∥
∥![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
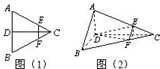 已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足