题目内容
函数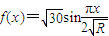 的一个最大值点和相邻最小值点恰在圆x2+y2=R2(R>0)上,则R=( )
的一个最大值点和相邻最小值点恰在圆x2+y2=R2(R>0)上,则R=( )A.
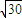
B.6
C.5
D.2π
【答案】分析:先用R表示出周期,得到最大值点和最小值点的坐标后,代入到圆的方程可求出R的值,最后可得答案
解答:解:∵x2+y2=R2,∴x∈[-R,R].
∵函数 的最小正周期为4
的最小正周期为4 ,
,
∴最大值点为( ,
, ),相邻的最小值点为(-
),相邻的最小值点为(- ,-
,- )
)
代入圆的方程,得R=6,
故选B.
点评:题主要考查三角函数的性质:周期性的应用.解题的关键是灵活利用三角函数两相邻的最大值与最小值正好等于半个周期的性质.
解答:解:∵x2+y2=R2,∴x∈[-R,R].
∵函数
 的最小正周期为4
的最小正周期为4 ,
,∴最大值点为(
 ,
, ),相邻的最小值点为(-
),相邻的最小值点为(- ,-
,- )
)代入圆的方程,得R=6,
故选B.
点评:题主要考查三角函数的性质:周期性的应用.解题的关键是灵活利用三角函数两相邻的最大值与最小值正好等于半个周期的性质.

练习册系列答案
相关题目
 的一个最大值点和相邻最小值点恰在圆x2+y2=R2(R>0)上,则R=
的一个最大值点和相邻最小值点恰在圆x2+y2=R2(R>0)上,则R=
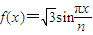 的一个最大值点和一个最小值点,则正整数的最小值是( )
的一个最大值点和一个最小值点,则正整数的最小值是( )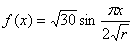 的一个最大值点和一个最小值点,则r的取值范围是
的一个最大值点和一个最小值点,则r的取值范围是

 ,+∞)
,+∞)