题目内容
已知曲线y=xlnx(x>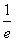 )在点(t,tlnt)处的切线l交x轴于点A,交y轴于点B,△AOB(O为坐标原点)的面积为S,
)在点(t,tlnt)处的切线l交x轴于点A,交y轴于点B,△AOB(O为坐标原点)的面积为S,
(Ⅰ)试写出S关于t的函数关系式;
(Ⅱ)求面积S的最小值;
(Ⅲ)若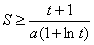 对于t>
对于t>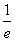 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
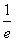 )在点(t,tlnt)处的切线l交x轴于点A,交y轴于点B,△AOB(O为坐标原点)的面积为S,
)在点(t,tlnt)处的切线l交x轴于点A,交y轴于点B,△AOB(O为坐标原点)的面积为S,(Ⅰ)试写出S关于t的函数关系式;
(Ⅱ)求面积S的最小值;
(Ⅲ)若
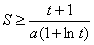 对于t>
对于t>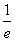 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。解:(Ⅰ)曲线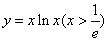 在点(t,tlnt)处的切线斜率为y′=1+lnt,
在点(t,tlnt)处的切线斜率为y′=1+lnt,
设 A(m,0),B(0,n),
则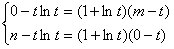 ,解得
,解得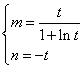 ,
,
所以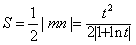 ,
,
注意到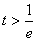 时,1+lnt>0,
时,1+lnt>0,
故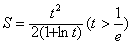 为所求;
为所求;
(Ⅱ)记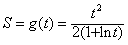 ,则S′=g′(t)=
,则S′=g′(t)=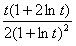 ,
,
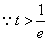 ,
,
∴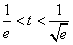 时,S′<0;
时,S′<0;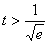 时,S′>0,
时,S′>0,
即函数S=g(t)在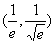 上单调递减,在
上单调递减,在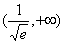 上单调递增,
上单调递增,
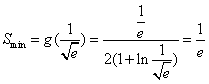 ,
,
所以面积S的最小值为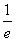 ,当且仅当
,当且仅当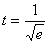 时取到;
时取到;
(Ⅲ)由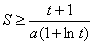 ,及1+lnt>0得,
,及1+lnt>0得,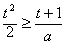 对t>
对t>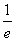 恒成立,
恒成立,
记u(t)=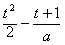 ,则u′(t)=
,则u′(t)=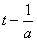 ,
,
当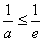 ,即a<0或a≥e时,u′(t)>0恒成立,
,即a<0或a≥e时,u′(t)>0恒成立,
此时u(t)在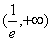 上单调递增,
上单调递增,
∴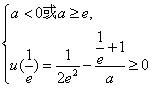 ,解得a<0或a≥2e2+2e,
,解得a<0或a≥2e2+2e,
当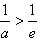 ,即0<a<e时,u′(t)>0
,即0<a<e时,u′(t)>0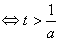 ,
,
所以函数u(t)在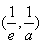 上单调递减,在
上单调递减,在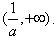 上单调递增,
上单调递增,
此时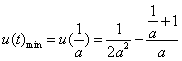 ,
,
∴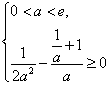 ,此方程无解;
,此方程无解;
综上,a<0或a≥2e2+2e为所求。
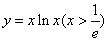 在点(t,tlnt)处的切线斜率为y′=1+lnt,
在点(t,tlnt)处的切线斜率为y′=1+lnt,设 A(m,0),B(0,n),
则
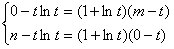 ,解得
,解得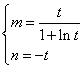 ,
,所以
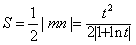 ,
,注意到
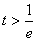 时,1+lnt>0,
时,1+lnt>0,故
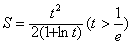 为所求;
为所求;(Ⅱ)记
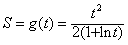 ,则S′=g′(t)=
,则S′=g′(t)=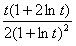 ,
,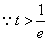 ,
,∴
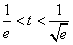 时,S′<0;
时,S′<0;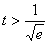 时,S′>0,
时,S′>0,即函数S=g(t)在
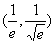 上单调递减,在
上单调递减,在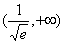 上单调递增,
上单调递增,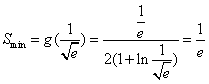 ,
,所以面积S的最小值为
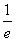 ,当且仅当
,当且仅当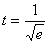 时取到;
时取到;(Ⅲ)由
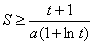 ,及1+lnt>0得,
,及1+lnt>0得,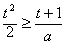 对t>
对t> 恒成立,
恒成立,记u(t)=
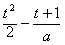 ,则u′(t)=
,则u′(t)=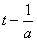 ,
,当
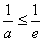 ,即a<0或a≥e时,u′(t)>0恒成立,
,即a<0或a≥e时,u′(t)>0恒成立,此时u(t)在
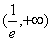 上单调递增,
上单调递增,∴
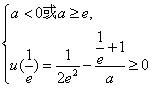 ,解得a<0或a≥2e2+2e,
,解得a<0或a≥2e2+2e,当
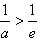 ,即0<a<e时,u′(t)>0
,即0<a<e时,u′(t)>0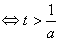 ,
,所以函数u(t)在
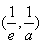 上单调递减,在
上单调递减,在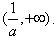 上单调递增,
上单调递增,此时
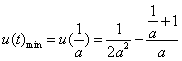 ,
,∴
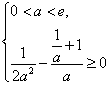 ,此方程无解;
,此方程无解;综上,a<0或a≥2e2+2e为所求。

练习册系列答案
相关题目
已知曲线C的方程为y=xlnx,则C上点x=1处的切线的倾斜角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|



