题目内容
已知P:|1-
|>2,Q:x2-2x+1-m2>0(m>0),且P是Q的充分不必要条件,求实数m的取值范围.
| x-1 | 3 |
分析:根据绝对值的性质和十字相乘法分别求出命题P和Q,根据P是Q的充分不必要条件可知P⇒Q,从而求出m的范围;
解答:解:∵P:|1-
|>2,
∴
>2或
<-2
解得,x>10或x<-2,
∴P=(-∞,-2)∪(10,+∞)
∵Q:x2-2x+1-m2>0(m>0),
[x-(m+1)][x-(1-m)]>0
解得x>1+m,x<1-m,
∴Q=(-∞,1-m)∪(1+m,+∞)
∵P是Q的充分不必要条件,
∴P⇒Q,∴P⊆Q,
∴
,
解得,m≤3,当m=3时,符合题意;
∴0<m≤3
| x-1 |
| 3 |
∴
| 4-x |
| 3 |
| 4-x |
| 3 |
解得,x>10或x<-2,
∴P=(-∞,-2)∪(10,+∞)
∵Q:x2-2x+1-m2>0(m>0),
[x-(m+1)][x-(1-m)]>0
解得x>1+m,x<1-m,
∴Q=(-∞,1-m)∪(1+m,+∞)
∵P是Q的充分不必要条件,
∴P⇒Q,∴P⊆Q,
∴
|
解得,m≤3,当m=3时,符合题意;
∴0<m≤3
点评:此题主要考查绝对值的性质和充分必要条件的定义,解题的过程中注意验证端点值,是一道基础题;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,x∈[
,x∈[ ,4].
,4]. );
); ,
,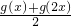 +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围. ,x∈[
,x∈[ ,4].
,4]. );
); ,
, ],则f1(x)=-1,x∈[-
],则f1(x)=-1,x∈[- ,
, ],f2(x)=sinx,x∈[-
],f2(x)=sinx,x∈[- ,
, ],设φ(x)=
],设φ(x)= +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.