题目内容
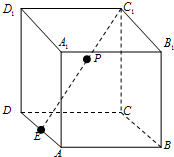
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )
| A.2 | B.
| C.
| D.
|

如图所示,取A1D1的中点F,连接EF,EC1,
∵EF∥CC1,EF=CC1=BB1,BB1⊥底面ABCD,
∴四边形EFB1B是矩形.
∴BB1∥EF,
又EF?平面C1EF,BB1?平面C1EF,∴BB1∥平面C1EF.
∴直线B1B上任一点到平面C1EF的距离是两条异面直线C1E与BB1的距离.
过点B1作B1M⊥C1F,
∵平面C1EF⊥平面A1B1C1D1.
∴B1M⊥平面C1EF.
过点M作MP∥EF交C1E于点P,则MP∥C1C.
取B1N=MP,连接PN,则四边形MPNB1是矩形.
可得NP⊥平面C1EF,
在△B1C1F中,B1M•C1F=B1C1•A1B1,又C1F=
=
,得B1M=
=
.
∴点P到直线CC1的距离的最小值为
.
故选:C.

∵EF∥CC1,EF=CC1=BB1,BB1⊥底面ABCD,
∴四边形EFB1B是矩形.
∴BB1∥EF,
又EF?平面C1EF,BB1?平面C1EF,∴BB1∥平面C1EF.
∴直线B1B上任一点到平面C1EF的距离是两条异面直线C1E与BB1的距离.
过点B1作B1M⊥C1F,
∵平面C1EF⊥平面A1B1C1D1.
∴B1M⊥平面C1EF.
过点M作MP∥EF交C1E于点P,则MP∥C1C.
取B1N=MP,连接PN,则四边形MPNB1是矩形.
可得NP⊥平面C1EF,
在△B1C1F中,B1M•C1F=B1C1•A1B1,又C1F=
AB2+(
|
| 10 |
| 3×2 | ||
|
3
| ||
| 5 |
∴点P到直线CC1的距离的最小值为
3
| ||
| 5 |
故选:C.


练习册系列答案
相关题目