题目内容
如图，四面体ABCD的每条棱长都等于2，点E，F分别为棱AB，AD的中点，则|| AB |
| BC |
2
2
，|| BC |
| EF |
| 3 |
| 3 |
分析：利用向量的加法法则化简
+
=
，再求其模即可；根据点E，F分别为棱AB，AD的中点，则
=
，然后根据向量的减法法则化简
-
，求出其模即可．
| AB |
| BC |
| AC |
| EF |
| 1 |
| 2 |
| BD |
| BC |
| EF |
解答：解：∵
+
=
，
∴|
+
|=|
|=2；
由于点E，F分别为棱AB，AD的中点，
则
=
，
∴|
-
|=|
-
|，取BD的中点H，
则|
-
|=|
-
|=|
-
|=|
|=
，
故答案为：2，
．
| AB |
| BC |
| AC |
∴|
| AB |
| BC |
| AC |
由于点E，F分别为棱AB，AD的中点，
则
| EF |
| 1 |
| 2 |
| BD |
∴|
| BC |
| EF |
| BC |
| 1 |
| 2 |
| BD |
则|
| BC |
| EF |
| BC |
| 1 |
| 2 |
| BD |
| BD |
| BH |
| HC |
| 3 |
故答案为：2，
| 3 |
点评：本题主要考查了向量在几何中的应用，以及向量的线性运算，同时考查了中位线的计算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
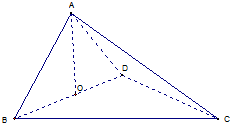如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，
如图，四面体ABCD中，0是BD的中点，CA=CB=CD=BD=a，AB=AD=
如图，四面体ABCD的各个面都是直角三角形，已知AB⊥BC，BC⊥CD，AB=a，BC=a，CD=c．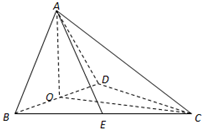
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．