题目内容
已知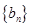 是公比大于
是公比大于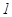 的等比数列,它的前
的等比数列,它的前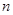 项和为
项和为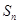 , 若
, 若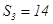 ,
,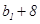 ,
,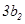 ,
,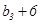 成等差数列,且
成等差数列,且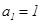 ,
,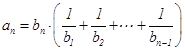 (
(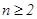 ).
).
(1)求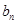 ;
;
(2)证明: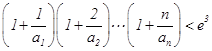 (其中
(其中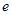 为自然对数的底数).
为自然对数的底数).
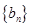 是公比大于
是公比大于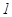 的等比数列,它的前
的等比数列,它的前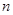 项和为
项和为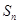 , 若
, 若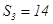 ,
,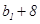 ,
,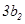 ,
,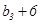 成等差数列,且
成等差数列,且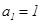 ,
,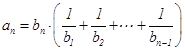 (
(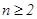 ).
).(1)求
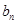 ;
;(2)证明:
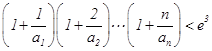 (其中
(其中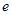 为自然对数的底数).
为自然对数的底数).(1)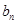
 ;(2)见解析
;(2)见解析
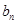
 ;(2)见解析
;(2)见解析(1)列出 ;(2)
;(2)
解:(1)依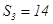 ,
,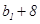 ,
,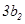 ,
,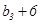 成等差数列,
成等差数列,
得 -----------------------------------------(2分)
-----------------------------------------(2分)
从而 得
得
故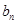
 .--------------------------------------------------------(4分)
.--------------------------------------------------------(4分)
(2)当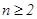 时,
时, 

得.
要证明
只需证 .--------------------(1分)
.--------------------(1分)
令 ,则
,则 =
=

于是
令 =
=
 =
=
得 =
=
故 =
=
故 .-------------------------------(3分)
.-------------------------------(3分)
 ;(2)
;(2)解:(1)依
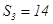 ,
,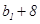 ,
,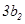 ,
,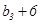 成等差数列,
成等差数列,得
 -----------------------------------------(2分)
-----------------------------------------(2分)从而
 得
得
故
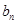
 .--------------------------------------------------------(4分)
.--------------------------------------------------------(4分)(2)当
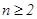 时,
时, 

得.

要证明

只需证
 .--------------------(1分)
.--------------------(1分)令
 ,则
,则 =
=

于是

令
 =
=
 =
=
得
 =
=
故
 =
=
故
 .-------------------------------(3分)
.-------------------------------(3分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
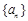 为等比数列,首项
为等比数列,首项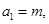 公比
公比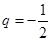 ,数列
,数列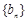 满足
满足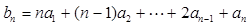 ,
,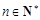 .
.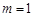 时,求
时,求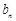 ;
;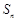 为数列
为数列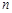 项和,若对于任意的正整数
项和,若对于任意的正整数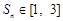 ,求实数
,求实数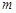 的取值范围.
的取值范围. 中,
中, .若
.若 ,数列
,数列 前
前 项的和为
项的和为 .
. ,求
,求 的解集.
的解集. ,求数列
,求数列 的前n项的和Tn。
的前n项的和Tn。 是由正数构成的等比数列,公比q=2。且
是由正数构成的等比数列,公比q=2。且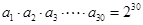 ,则
,则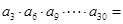 ( )
( )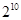
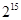
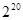
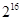
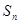 为等比数列
为等比数列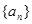 的前
的前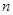 项和,
项和,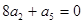 ,则
,则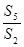 =( )
=( )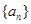 满足
满足 ,且
,且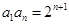 ,则
,则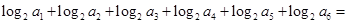 ( )
( ) 
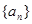 的前n项和为
的前n项和为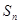 ,且
,且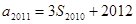 ,
, 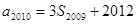 ,则公比
,则公比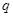 等于 ( )
等于 ( )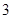
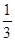
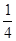
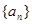 的前
的前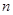 项和为
项和为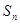 ,对任意
,对任意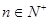 都有
都有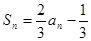 ,若
,若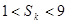
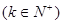 ,则
,则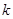 的值为___
的值为___  满足
满足 ,且
,且 ,则
,则 ( )
( )