题目内容
设F为抛物线x2=8y的焦点,点A,B,C在此抛物线上,若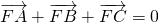 ,则
,则 =________.
=________.
12
分析:由题意可得 焦点F(0,2),准线为 y=-2,由条件可得F是三角形ABC的重心,可得 2= ,
,
由抛物线的定义可得 =(y1+2)+(y2+2)+(y3+2).
=(y1+2)+(y2+2)+(y3+2).
解答:由题意可得 p=4,焦点F(0,2),准线为 y=-2,由于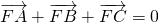 ,
,
故F是三角形ABC的重心,设 A、B、C 的纵坐标分别为 y1,y2,y3,
∴2= ,∴y1+y2+y3=6.
,∴y1+y2+y3=6.
由抛物线的定义可得 =(y1+2)+(y2+2)+(y3+2)=12.
=(y1+2)+(y2+2)+(y3+2)=12.
故答案为:12.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,得到 y1+y2+y3=6,是解题的关键.
分析:由题意可得 焦点F(0,2),准线为 y=-2,由条件可得F是三角形ABC的重心,可得 2=
 ,
,由抛物线的定义可得
 =(y1+2)+(y2+2)+(y3+2).
=(y1+2)+(y2+2)+(y3+2).解答:由题意可得 p=4,焦点F(0,2),准线为 y=-2,由于
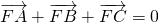 ,
,故F是三角形ABC的重心,设 A、B、C 的纵坐标分别为 y1,y2,y3,
∴2=
 ,∴y1+y2+y3=6.
,∴y1+y2+y3=6.由抛物线的定义可得
 =(y1+2)+(y2+2)+(y3+2)=12.
=(y1+2)+(y2+2)+(y3+2)=12.故答案为:12.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,得到 y1+y2+y3=6,是解题的关键.

练习册系列答案
相关题目
 设b>0,椭圆方程为
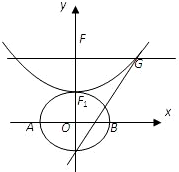
设b>0,椭圆方程为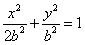 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,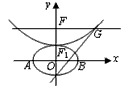
 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.