Question

已知△ABC是边长为4

2

的正三角形，SC⊥面ABC，SC=2，E、D分别为BC和AB的中点，则异面直线CD和SE之间距离

 

．

Answer 1

分析：取F为BD的中点，连接EF，易得EF∥CD，故可将异面直线CD和SE之间距离，转化为直线CD与平面SEF的距离，即C到平面SEF的距离，进而利用等积法，求出答案．

解答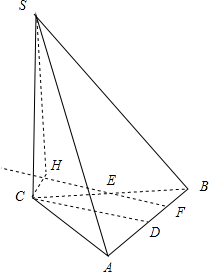：解：取F为BD的中点，连接EF，则EF∥CD
又∵CD?平面SEF，EF?平面SEF
∴CD∥平面SEF
故异面直线CD和SE之间距离即为直线CD与平面SEF的距离
则C到平面SEF的距离d即为异面直线CD和SE之间距离
过C作CH垂直EF，连接SH，则SH⊥EF
∵SH=

SC2+CH2

=

SC2+DF2

=

6

∵△ABC是边长为4

2

的正三角形，故S_△CEF=

1

8

S_△ABC=

3

故四棱锥S-CEF的体积V=

1

3

•S_△CEF•SC=

1

3

•

3

•2=

2 3

3

又∵S_△SEF=

1

2

EF•SH=

1

2

•（

1

2

×

3

2

×4

2

）•

6

=3
故

1

3

•S_△SEF•h=

2 3

3

故h=

2 3

3

故答案为：

2 3

3

点评：本题考查的知识点是异面直线的距离，其中将异面直线距离转化为线面距离和点到平面的距离是解答的关键．