题目内容
设 是公差为正数的等差数列,
是公差为正数的等差数列, 则
则 ( )
( )
| A.40 | B.50 | C.60 | D.70 |
C.
解析试题分析: 故选C.
故选C.
考点:1.等差数列的性质;2.求等差数列若干项的和.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知等差数列 的前n项和为
的前n项和为 等于( )
等于( )
| A.-90 | B.-27 | C.-25 | D.0 |
已知数列 为等比数列,且
为等比数列,且 ,设等差数列
,设等差数列 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =( )
=( )
| A.36 | B.32 | C.24 | D.22 |
如果等差数列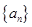 中,
中, ,那么
,那么 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
在等差数列 中,
中, ,则前13项之和等于( )
,则前13项之和等于( )
A. | B. | C. | D. |
等差数列 中,已知前15项的和
中,已知前15项的和 ,则
,则 等于( )
等于( )
A. | B.12 | C. | D.6 |
在数列 中,
中,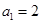 ,
,  ,则
,则 ( )
( )
A. | B. | C. | D. |
等差数列
 中,已知
中,已知 ,且在前
,且在前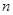 项和
项和 中,仅当
中,仅当 时,
时, 最大,则公差d满足( )
最大,则公差d满足( )
A. | B. |
C. | D. |
已知等差数列 满足
满足 ,
, ,则数列
,则数列 的前10项的和等于( )
的前10项的和等于( )
| A.23 | B.95 | C.135 | D.138 |