题目内容
【题目】如图,直线![]() 与圆
与圆 ![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点.
两点.

(1)若直线![]() 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长![]()
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,判断
,判断![]() 是否为定值,并说明理由
是否为定值,并说明理由
(3)求![]() ,面积的最小值.
,面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由题意设直线![]() 由直线与圆相切可得
由直线与圆相切可得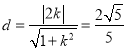 ,可得
,可得![]() ,故分两种情况可求得
,故分两种情况可求得![]() 。(2)(ⅰ)当直线
。(2)(ⅰ)当直线![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;(ⅱ)当
;(ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 将其代入圆的方程得
将其代入圆的方程得![]() ,根据斜率公式及根与系数的关系计算可得
,根据斜率公式及根与系数的关系计算可得![]() 。从而可得
。从而可得![]() 。(3)(ⅰ)当
。(3)(ⅰ)当![]() 斜率不存在或为
斜率不存在或为![]() 时,可得
时,可得![]() 。当
。当![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设直线
时,设直线![]() ,可求得
,可求得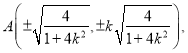 点B的坐标为
点B的坐标为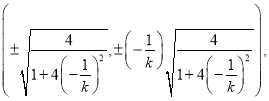
故可得![]()
![]() ,令
,令![]() ,则
,则![]()
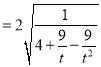 ,故当
,故当![]()
![]() 有最小值,且
有最小值,且 ![]() .
.
试题解析:
(1)由题意直线![]() 斜率存在,设直线
斜率存在,设直线![]()
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以
解得![]()
当![]() 时,由
时,由 解得
解得![]() ,所以
,所以![]()
当![]() 时,同理
时,同理![]()
所以![]() 。
。
(2)(ⅰ)当直线![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;
;
(ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]()
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以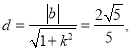
整理得所以![]() ①,
①,
由![]() 消去y整理得
消去y整理得![]() ,
,
由直线与圆相交得![]()
设![]()
则![]()
![]() ,②
,②
所以![]() ③,
③,
将①②代入③式得![]()
综上可得![]()
(3)由(2)知![]()
法一:(ⅰ)当![]() 斜率不存在或为
斜率不存在或为![]() 时,可得
时,可得![]() ,
,
(ⅱ)当![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设直线
时,设直线![]() ,
,
由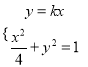 ,解得
,解得
所以点A的坐标为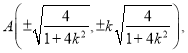
同理点B的坐标为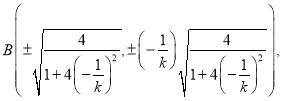
所以![]()
![]() ,
,
令![]() ,
,
所以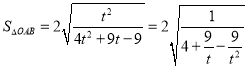 ,
,
故当![]()
![]() 有最小值,且
有最小值,且 ![]() .
.
综上可得![]() 面积的最小值为
面积的最小值为![]() 。
。
法二:记直线![]() 与圆
与圆![]() 的切点为
的切点为![]()
设![]()
所以![]() ,
,
则![]()
所以当![]() 时,
时, ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目