题目内容
讨论下列函数在x0=2处的连续性:(1)f(x)=x2;
(2)f(x)=![]() ;
;
(3)f(x)=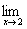
(4)f(x)=![]()
分析:严格按连续性定义求解.
解:(1)![]() f(x)=
f(x)=![]() x2=4=f(2),所以f(x)在x0=2处连续.
x2=4=f(2),所以f(x)在x0=2处连续.
(2)函数f(x)在x=2处没有定义,所以函数f(x)在x0=2处不连续.
(3)![]() f(x)=4≠f(2)=1,所以函数f(x)在x0=2处不连续.
f(x)=4≠f(2)=1,所以函数f(x)在x0=2处不连续.
(4)![]() f(x)=
f(x)=![]() 2=2,
2=2,![]() f(x)=
f(x)=![]() (-2)=-2,所以
(-2)=-2,所以![]() f(x)不存在,所以f(x)在x0=2处不连续.
f(x)不存在,所以f(x)在x0=2处不连续.

练习册系列答案
相关题目