题目内容
(满分12分)如图所示,在四棱锥P-ABCD中,![]() 平面ABCD,PC=2,在四边形ABCD中,
平面ABCD,PC=2,在四边形ABCD中,![]() ,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成
,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成![]() 的角.
的角.
(1)求证:![]() // 平面PAD;
// 平面PAD;
(2)点C到平面PAD的距离.
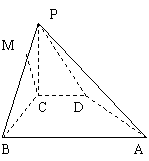 |
解:以点C为空间直角坐标系的坐标原点,CB为x轴,CD为y轴,CP为z轴建如图所示的空间直角坐标系C-xyz,
(1) 因为![]() 平面ABCD,
平面ABCD, ![]() 为PB与平面ABCD成的角,
为PB与平面ABCD成的角,![]()
![]()
因为PC=2, ![]() ,PB=4
,PB=4![]() ,
,
![]()
(法一)可直接求平面PAD的法向量![]() 的坐标,证明
的坐标,证明![]() 即可
即可
(法二):也可令![]() ,即
,即![]()
解得![]()
![]() ,故
,故![]() 共面,
共面,
又因为![]() 平面PAD,
平面PAD,![]() 平面PAD;
平面PAD;
取AP的中点,则![]() 因为PB=AB,
因为PB=AB,![]()
又因为![]()
![]() ,
,![]() 平面PAD;
平面PAD;
![]() 平面PAD, 又因为
平面PAD, 又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面PAD;
平面PAD;
(2)由上面得![]() 平面PAD,
平面PAD, ![]()
![]() 是平面PAD的法向量,
是平面PAD的法向量,
![]() 平面PAD的单位法向量为
平面PAD的单位法向量为 ,又因为
,又因为![]()
![]() 点C到平面PAD的距离为d=
点C到平面PAD的距离为d=![]()

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 中,
中, ,
,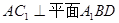 ,
, 的中点.
的中点.
 ∥
∥ ;
; ;
; 上是否存在一点
上是否存在一点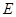 ,使得
,使得 ,若存在,试确定
,若存在,试确定 是否垂直?若不存在,请说明理由.
是否垂直?若不存在,请说明理由. 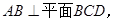 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC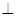 CD.
CD.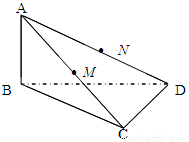
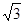 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. (1)求证:PO⊥面ABCE;
(1)求证:PO⊥面ABCE; 的正弦值.
的正弦值. 中,底面边长为
中,底面边长为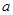 ,侧棱长为
,侧棱长为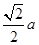 ,
,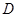 是棱
是棱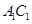 的中点.
的中点. 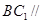 平面
平面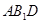 ;
;
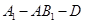 的大小;[来源:ZXXK]
的大小;[来源:ZXXK]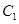 到平面
到平面