题目内容
若α是三角形的一个内角,当α=
arccos
| 3 |
| 4 |
arccos
时,函数y=cos2α-3cosα+6取到最小值.(结果用反三角函数表示).| 3 |
| 4 |
分析:利用二倍角余弦公式将y=cos2α-3cosα+6化成y=2(cosα-
)2+
,利用二次函数性质及反三角函数表示法求出即可.
| 3 |
| 4 |
| 31 |
| 8 |
解答:解:y=cos2α-3cosα+6=2cos2α-3cosα+5=2(cosα-
)2+
∵α是三角形的一个内角,∴0<cosα<1,当cosα=
时,函数取到最小值,
根据反三角函数表示法,可得α=arccos
.
故答案为:arccos
.
| 3 |
| 4 |
| 31 |
| 8 |
∵α是三角形的一个内角,∴0<cosα<1,当cosα=
| 3 |
| 4 |
根据反三角函数表示法,可得α=arccos
| 3 |
| 4 |
故答案为:arccos
| 3 |
| 4 |
点评:本题考查二倍角余弦公式,二次函数性质及反三角函数知识,属于常规题.

练习册系列答案
相关题目
 =2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则
=2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则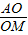 = ”.
= ”. ,那么这个球的表面积是 .
,那么这个球的表面积是 .