题目内容
()(本小题满分12分)
数列{an}的前N项和为Sn,a1=1,an+1=2Sn (n∈N*).
(I)求数列{an}的通项an;
(II)求数列{nan}的前n项和T.
an=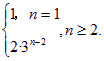 , Tn=
, Tn=![]() +(n-
+(n-![]() )3n-1(n∈N*)
)3n-1(n∈N*)
解析:
解:(I)∵an+1=2Sn,,
∴Sn+1-Sn=2Sn,
∴![]() =3.
=3.
又∵S1=a1=1,
∴数列{Sn}是首项为1、公比为3的等比数列,Sn=3n-1(n∈N*).
∴当n![]() 2时,an-2Sn-1=2·3n-2(n
2时,an-2Sn-1=2·3n-2(n![]() 2),
2),
∴an=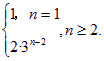
![]()
(II)Tn=a1+2a2+3a3+…+nan.
当n=1时,T1=1;
当n![]() 2时,Tn=1+4·30+6·31+2n·3 n-2,…………①
2时,Tn=1+4·30+6·31+2n·3 n-2,…………①
3Tn=3+4·31+6·32+…+2n·3n-1,…………②
①-②得:-2Tn=-2+4+2(31+32+…+3n-2)-2n·3 n-1
=2+2·![]()
=-1+(1-2n)·3n-1
∴Tn=![]() +(n-
+(n-![]() )3n-1 (n
)3n-1 (n![]() 2).
2).
又∵Tn=a1=1也满足上式,
∴Tn=![]() +(n-
+(n-![]() )3n-1(n∈N*)
)3n-1(n∈N*)

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 内的随机点,求函数
内的随机点,求函数