题目内容
已知椭圆Γ: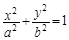 (a>b>0)经过D(2,0),E(1,
(a>b>0)经过D(2,0),E(1,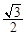 )两点.
)两点.
(1)求椭圆Γ的方程;
(2)若直线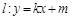 与椭圆Γ交于不同两点A,B,点G是线段AB中点,点O是坐标原点,设射线OG交Γ于点Q,且
与椭圆Γ交于不同两点A,B,点G是线段AB中点,点O是坐标原点,设射线OG交Γ于点Q,且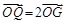 .
.
①证明: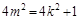
②求△AOB的面积.
(1)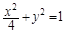 ;(2)
;(2)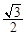
解析试题分析:(1)由已知M是PD的中点,利用P点在圆上,可以求出M的点轨迹方程为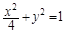 ;(2)点Q在(1)中的椭圆上,G是OQ的中点,利用直线与椭圆的关系及中点坐标公式,即可找到k与m的关系,并进一步求出三角形AOB的面积.
;(2)点Q在(1)中的椭圆上,G是OQ的中点,利用直线与椭圆的关系及中点坐标公式,即可找到k与m的关系,并进一步求出三角形AOB的面积.
试题解析:(1)由题意,得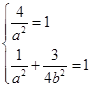 ,解得
,解得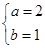
∴轨迹Γ的方程为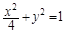 ; 5分
; 5分
(2)①令
由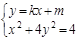 消去y
消去y
得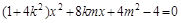 6分
6分
∴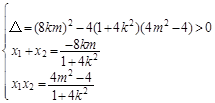 ,即
,即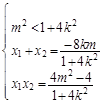 (1)
(1)
∴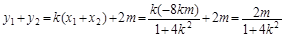
又由中点坐标公式,得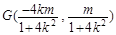
将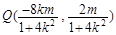 代入椭圆方程,有
代入椭圆方程,有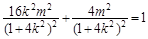
化简得: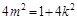 (2) 9分
(2) 9分
②由(1)(2)得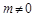
且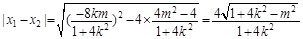 (3)
(3)
在△AOB中,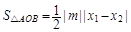 (4) 12分
(4) 12分
∴由(2)(3)(4)可得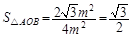
∴△AOB的面积是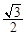 13分
13分
考点:动点轨迹,直线与椭圆的位置关系,中点坐标,平面向量的坐标运算,三角形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
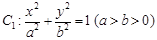 的离心率为
的离心率为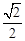 ,
,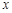 轴被曲线
轴被曲线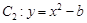 截得的线段长等于
截得的线段长等于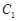 的短轴长.
的短轴长.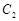 与
与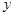 轴的交点为
轴的交点为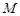 ,过坐标原点
,过坐标原点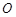 的直线
的直线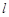 与
与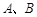 ,直线
,直线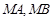 分别与
分别与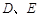 .
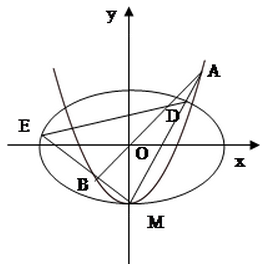
.
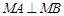 ;
;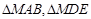 的面积分别为
的面积分别为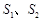 ,若
,若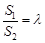 ,求
,求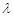 的取值范围.
的取值范围.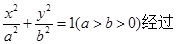 点
点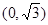 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为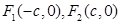
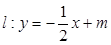 与椭圆交于
与椭圆交于 两点,与以
两点,与以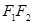 为直径的圆交于
为直径的圆交于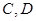 两点,且满足
两点,且满足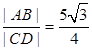 ,求直线
,求直线 的方程.
的方程.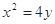 ,过点
,过点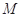
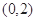 作直线与抛物线交于两点
作直线与抛物线交于两点 ,
,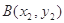 ,过
,过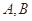 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为 .
.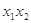 的值;
的值;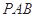 面积的最小值.
面积的最小值.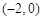 ,
,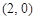 ,并且经过点
,并且经过点 ,求它的标准方程.
,求它的标准方程. ,0)和F2(
,0)和F2(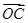 ·
·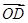 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程. 的一个焦点为
的一个焦点为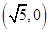 ,离心率为
,离心率为 .
. 的标准方程;
的标准方程;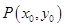 为椭圆
为椭圆 到椭圆
到椭圆 的焦点为
的焦点为