题目内容
给出下列命题:①若|
|=|
|,则
=
或
=-
;②|
•
|=|
||
|;③
•
=0?
=0或
=0;④若
∥
且
∥
,则
∥
.其中正确命题的个数是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| c |
| a |
| c |
| A、0 | B、1 | C、2 | D、3 |
分析:由|
|=|
|,故不能推出
=
或
=-
,故①不正确;由两个向量的数量积的定义可得②不正确;由
•
=0 可得
⊥
,不能推出
=0或
=0故③不正确;通过举反例可得④不正确.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:解:①不正确,|
|=|
|,说明
,
的长度相等,但它们的方向是不确定的,故不能推出
=
或
=-
.
②不正确,由两个向量的数量积的定义可得|
•
|=|
|•|
|•|cos<
,
>.
③不正确,由
•
=0 可得
⊥
,故不能推出
=0或
=0.
④不正确,当
=
时,对任意的向量
和
,都有
∥
且
∥
,故不能推出
∥
.
故选 A.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②不正确,由两个向量的数量积的定义可得|
| a |
| b |
| a |
| b |
| a |
| b |
③不正确,由
| a |
| b |
| a |
| b |
| a |
| b |
④不正确,当
| b |
| 0 |
| a |
| b |
| a |
| b |
| b |
| c |
| a |
| c |
故选 A.
点评:本题考查两个向量的数量积公式,两个向量共线的性质和条件,相等的向量、相反的向量,准确把握有关概念,
是解题的关键.
是解题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
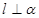 ,则
,则 则
则 在平面
在平面 。
。 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质: ; (2)
; (2) ; (3)
; (3) .
. :
: ,则
,则 ;
; ,且
,且 ,则a = 0;
,则a = 0; ,且
,且 ,
, ,则a = c.
,则a = c. 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 与
与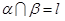 ,若
,若 ;4直线
;4直线 的充要条件是
的充要条件是 、
、 ,且m⊥
,且m⊥ ,
,