题目内容
某工厂生产甲、乙两种产品，其产量分别为45个与55个，所用原料分别为A、B两种规格的金属板，每张面积分别为2 m2与3 m2.用A种规格的金属板可造甲种产品3个，乙种产品5个；用B种规格的金属板可造甲、乙种产品各6个.问A、B两种规格金属板各取多少张，才能完成计划，并使总的用料面积最省？
解：设A、B两种金属板各取x张、y张，用料面积z,则约束条件为
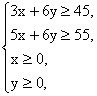
目标函数z=2x+3y.
作出以上不等式组所表示的平面区域，即可行域，如图所示.
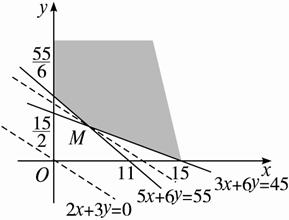
z=2x+3y变为y=-
x+
，得斜率为-
，在y轴上的截距为
，且随z变化的一组平行线.
当直线z=2x+3y过可行域上的点M时，截距最小，z最小.
解方程组
得M点的坐标为(5,5).
此时zmin=2×5+3×5=25(m2).
答：两种金属板各取5张时，用料面积最省.
练习册系列答案
相关题目
18、某工厂生产甲、乙两种产品，每种产品都是经过第一道和第二道工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级，对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品