题目内容
 已知函数f(x)=2cos(ωx+φ)(ω>0,-π<φ<0)的最小正周期为π,其图象的一条对称轴是直线
已知函数f(x)=2cos(ωx+φ)(ω>0,-π<φ<0)的最小正周期为π,其图象的一条对称轴是直线 .
.
(Ⅰ)求ω,φ;
(Ⅱ)求函数y=f(x)的单调递减区间;
(Ⅲ)画出函数y=f(x)在区间[0,π]上的图象.
(Ⅰ)由题意可得  =π,∴ω=2.
=π,∴ω=2.
∵图象的一条对称轴是直线 ,
,
∴2cos(2× +φ)=±2.
+φ)=±2.
再由,-π<φ<0可得 φ=- ,
,
∴函数f(x)=2cos(2x- ).
).
(Ⅱ)令 2kπ≤2x- ≤2kπ+π,k∈z,解得 kπ+
≤2kπ+π,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,故函数的减区间为[kπ+
,k∈z,故函数的减区间为[kπ+ ,kπ+
,kπ+ ],k∈z.
],k∈z.
(Ⅲ)列表:
画出函数y=f(x)在区间[0,π]上的图象,如图所示:
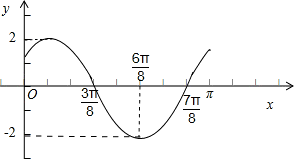
分析:(Ⅰ)由周期求得ω=2,由图象的对称轴方程以及φ的范围求出 φ=- ,从而得到 函数f(x)=2cos(2x-
,从而得到 函数f(x)=2cos(2x- ).
).
(Ⅱ)令 2kπ≤2x- ≤2kπ+π,k∈z,求出x的范围,即可求得函数的减区间.
≤2kπ+π,k∈z,求出x的范围,即可求得函数的减区间.
(Ⅲ)列表,根据列表画出函数的图象.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.
 =π,∴ω=2.
=π,∴ω=2.∵图象的一条对称轴是直线
 ,
,∴2cos(2×
 +φ)=±2.
+φ)=±2.再由,-π<φ<0可得 φ=-
 ,
,∴函数f(x)=2cos(2x-
 ).
).(Ⅱ)令 2kπ≤2x-
 ≤2kπ+π,k∈z,解得 kπ+
≤2kπ+π,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,故函数的减区间为[kπ+
,k∈z,故函数的减区间为[kπ+ ,kπ+
,kπ+ ],k∈z.
],k∈z.(Ⅲ)列表:
| x | 0 |  | 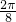 |  | 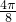 |  | 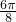 |  | π |
2x- | - | 0 |  |  |  | π |  |  |  |
| f(x) |  | 2 |  | 0 |  | -2 | - | 0 |  |

分析:(Ⅰ)由周期求得ω=2,由图象的对称轴方程以及φ的范围求出 φ=-
 ,从而得到 函数f(x)=2cos(2x-
,从而得到 函数f(x)=2cos(2x- ).
).(Ⅱ)令 2kπ≤2x-
 ≤2kπ+π,k∈z,求出x的范围,即可求得函数的减区间.
≤2kπ+π,k∈z,求出x的范围,即可求得函数的减区间.(Ⅲ)列表,根据列表画出函数的图象.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目