题目内容
17.已知数列{an}中,a1=3,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$,则其通项公式为an=$\frac{3}{6n-5}$.分析 把已知的数列递推式取倒数,可得数列{$\frac{1}{{a}_{n}}$}是以$\frac{1}{3}$为首项,以2为公差的等差数列,求出等差数列的通项公式可得数列{an}的通项an.
解答 解:由an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$,得$\frac{1}{{a}_{n+1}}=\frac{1}{{a}_{n}}+2$,
即$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}=2$,
又a1=3,∴$\frac{1}{{a}_{1}}=\frac{1}{3}$,
则数列{$\frac{1}{{a}_{n}}$}是以$\frac{1}{3}$为首项,以2为公差的等差数列,
∴$\frac{1}{{a}_{n}}=\frac{1}{3}+2(n-1)=\frac{6n-5}{3}$,
则${a}_{n}=\frac{3}{6n-5}$.
故答案为:$\frac{3}{6n-5}$.
点评 本题考查了数列递推式,考查了等差关系的确定,考查了等差数列的通项公式,是中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
5.已知函数f(x)=asinx-$\sqrt{3}$cosx的一条对称轴为x=-$\frac{π}{6}$,且f(x1)•f(x2)=-4,则|x1+x2|的最小值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2}{3}π$ | D. | $\frac{4}{3}π$ |
2.执行如图的程序框图,当输入25时,则该程序运行后输出的结果是( )
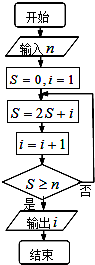

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
9.若集合A={0,1,2},B={x|x2<3},则A∩B=( )
| A. | ∅ | B. | {-1,0,1} | C. | {0,1,2} | D. | {0,1} |