题目内容
过坐标原点作函数y=lnx图象的切线.则切线斜率为 .
分析:欲求切点的坐标,先设切点的坐标为(x0,y0),再求出在点切点(x0,y0),的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=x0处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用切线过原点即可解决问题.
解答:解:设切点的坐标为(x0,y0),切线的斜率为k,
由于y′=
,则k故切线方程为y-y0=
(x-x0)
又切线过原点,∴-y0=
(-x0),解得y0=1,则x0=e,
故k=
=
.
故答案为:
.
由于y′=
| 1 |
| x |
| 1 |
| x0 |
又切线过原点,∴-y0=
| 1 |
| x0 |
故k=
| 1 |
| x0 |
| 1 |
| e |
故答案为:
| 1 |
| e |
点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
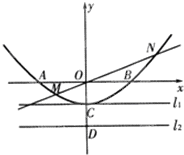 如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线
如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线