题目内容
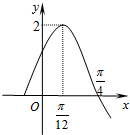 已知定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0)的一段图象如图所示.
已知定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0)的一段图象如图所示.
(1)求f(x)的解析式;
(2)若g(x)=cos3x,h(x)=f(x)•g(x),求函数h(x)的单调递增区间.
解:(1)∵T=( -
- )=
)= ,
,
∴ω= =3,
=3,
∴f(x)=2sin(3x+φ).
∵点( ,2)在图象上,
,2)在图象上,
∴2sin(3× +φ)=2,即sin(φ+
+φ)=2,即sin(φ+ )=1,
)=1,
∴φ+ =2kπ+
=2kπ+ (k∈Z),即φ=2kπ+
(k∈Z),即φ=2kπ+ .
.
故f(x)=2sin(3x+ ).(6分)
).(6分)
(2)h(x)=2sin(3x+ )cos3x
)cos3x
=2(sin3xcos +cos3xsin
+cos3xsin )cos3x
)cos3x
= (six3xcos3x+cos23x)
(six3xcos3x+cos23x)
= (sin6x+cos6x+1)
(sin6x+cos6x+1)
=sin(6x+ )+
)+ .
.
由2kπ- ≤6x+
≤6x+ ≤2kπ+
≤2kπ+ (k∈Z)得函数h(x)的单调递增区间为[
(k∈Z)得函数h(x)的单调递增区间为[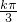 -
- ,
,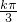 +
+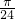 ](k∈Z).(12分)
](k∈Z).(12分)
分析:(1)由图可求得其周期T,继而可求得ω,再利用点( ,2)在图象上可求得φ,从而可求得其解析式;
,2)在图象上可求得φ,从而可求得其解析式;
(2)利用三角函数间的关系及倍角公式,辅助角公式可求得h(x)=sin(6x+ )+
)+ ,利用正弦函数的单调性即可求得h(x)的单调递增区间.
,利用正弦函数的单调性即可求得h(x)的单调递增区间.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查三角函数中的恒等变换应用及正弦函数的单调性,考查化归思想与综合运算能力,属于难题.
 -
- )=
)= ,
,∴ω=
 =3,
=3,∴f(x)=2sin(3x+φ).
∵点(
 ,2)在图象上,
,2)在图象上,∴2sin(3×
 +φ)=2,即sin(φ+
+φ)=2,即sin(φ+ )=1,
)=1,∴φ+
 =2kπ+
=2kπ+ (k∈Z),即φ=2kπ+
(k∈Z),即φ=2kπ+ .
.故f(x)=2sin(3x+
 ).(6分)
).(6分)(2)h(x)=2sin(3x+
 )cos3x
)cos3x=2(sin3xcos
 +cos3xsin
+cos3xsin )cos3x
)cos3x=
 (six3xcos3x+cos23x)
(six3xcos3x+cos23x)=
 (sin6x+cos6x+1)
(sin6x+cos6x+1)=sin(6x+
 )+
)+ .
.由2kπ-
 ≤6x+
≤6x+ ≤2kπ+
≤2kπ+ (k∈Z)得函数h(x)的单调递增区间为[
(k∈Z)得函数h(x)的单调递增区间为[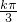 -
- ,
,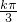 +
+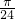 ](k∈Z).(12分)
](k∈Z).(12分)分析:(1)由图可求得其周期T,继而可求得ω,再利用点(
 ,2)在图象上可求得φ,从而可求得其解析式;
,2)在图象上可求得φ,从而可求得其解析式;(2)利用三角函数间的关系及倍角公式,辅助角公式可求得h(x)=sin(6x+
 )+
)+ ,利用正弦函数的单调性即可求得h(x)的单调递增区间.
,利用正弦函数的单调性即可求得h(x)的单调递增区间.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查三角函数中的恒等变换应用及正弦函数的单调性,考查化归思想与综合运算能力,属于难题.

练习册系列答案
相关题目