题目内容
设点 对应的复数为
对应的复数为 ,以原点为极点,实轴正半轴为极轴建立极坐标系,则点
,以原点为极点,实轴正半轴为极轴建立极坐标系,则点 的极坐标可能为( )
的极坐标可能为( )
A.(3, ) ) | B.(3, ) ) | C.( , , ) ) | D.( , , ) ) |
C
解析试题分析:点 对应的复数为
对应的复数为 ,所以P(-3,3),其极坐标为(
,所以P(-3,3),其极坐标为( ,
, ),选C。
),选C。
考点:复数的几何意义,点的极坐标。
点评:简单题,直角坐标化为极坐标,结合点的位置,应用公式 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知复数 (
( 为虚数单位),则复数
为虚数单位),则复数 的共轭复数的虚部为 ( )
的共轭复数的虚部为 ( )
A. | B.1 | C. | D. |
复数 ( )
( )
A. | B. | C. | D. |
若复数 满足方程
满足方程 ,则
,则
A. | B. | C. | D. |
已知复数 等于
等于
A. | B.6 | C. | D. |
复数 为纯虚数,则实数
为纯虚数,则实数 ( )
( )
| A.2 | B. | C. | D. |
若复数 ,则复数
,则复数 对应的点位于
对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
复数z=(m-2013)+(m-1)i表示纯虚数时,实数m为( )
| A.1 | B.-1 | C.2013 | D.-2013 |
复数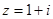 ,
,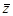 为
为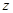 的共轭复数,则
的共轭复数,则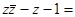 ( )
( )
| A.-2i | B.–i | C.i | D.2i |