题目内容
已知数列{an}的前n项和Sn=n2+4n(n∈N*),数列{bn}为等比数列,且首项b1和公比q满足: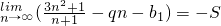
(I)求数列{an},{bn}的通项公式;
(II)设cn=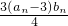 ,记数列{cn}的前n项和Tn,若不等式λ(an-2n)≤4Tn对任意n∈N*恒成立,求实数λ的最大值.
,记数列{cn}的前n项和Tn,若不等式λ(an-2n)≤4Tn对任意n∈N*恒成立,求实数λ的最大值.
解:(Ⅰ)当n=1时,a1=S1=5.
当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
验证n=1时也成立.
∴数列{an}的通项公式为:an=2n+3(n∈N*).
∵
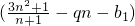
=
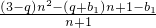 =-5,
=-5,
∴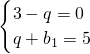 ,解得:b1=2,q=3.
,解得:b1=2,q=3.
∴数列{bn}的通项公式为:bn=2•3n-1.(5分)
(Ⅱ)∵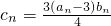 =n•3n,
=n•3n,
∴Tn=c1+c2+c3+…+cn
=3+2•32+3•33+…+n•3n①
3Tn=32+2•3n+3•34+…+n•3n+1②
由①-②得:-2Tn=3+32+…+3n-n•3n+1
=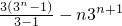
=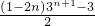 ,
,
∴ .(8分)
.(8分)
不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,(*)
设f (n)=(2n-1)•3n+1,
易知函数f (n)在n∈N*上单调递增,
故当n=1时(2n-1)•3n+1取得最小值为4,
∴由题意可知:不等式(*)对一切n∈N*恒成立,只需λ≤4.
∴实数λ的最大值为4.(12分)
分析:(Ⅰ)当n=1时,a1=S1=5.当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,验证n=1时也成立.由此能求出数列{an},{bn}的通项公式.
(Ⅱ)由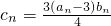 =n•3n,知Tn═3+2•32+3•33+…+n•3n,利用错位相减法能求出
=n•3n,知Tn═3+2•32+3•33+…+n•3n,利用错位相减法能求出 .不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,由此能求出实数λ的最大值.
.不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,由此能求出实数λ的最大值.
点评:本题考查数列的通项公式的求法,求实数λ的最大值.综合性强,难度大,是高考的重点,易错点是不等式λ(an-2n)≤4Tn化为λ≤(2n-1)•3n+1.解题时要认真审题,仔细解答,注意极限的合理运用.
当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
验证n=1时也成立.
∴数列{an}的通项公式为:an=2n+3(n∈N*).
∵

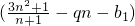
=

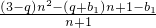 =-5,
=-5,∴
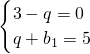 ,解得:b1=2,q=3.
,解得:b1=2,q=3.∴数列{bn}的通项公式为:bn=2•3n-1.(5分)
(Ⅱ)∵
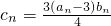 =n•3n,
=n•3n,∴Tn=c1+c2+c3+…+cn
=3+2•32+3•33+…+n•3n①
3Tn=32+2•3n+3•34+…+n•3n+1②
由①-②得:-2Tn=3+32+…+3n-n•3n+1
=
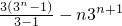
=
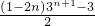 ,
,∴
 .(8分)
.(8分)不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,(*)
设f (n)=(2n-1)•3n+1,
易知函数f (n)在n∈N*上单调递增,
故当n=1时(2n-1)•3n+1取得最小值为4,
∴由题意可知:不等式(*)对一切n∈N*恒成立,只需λ≤4.
∴实数λ的最大值为4.(12分)
分析:(Ⅰ)当n=1时,a1=S1=5.当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,验证n=1时也成立.由此能求出数列{an},{bn}的通项公式.
(Ⅱ)由
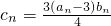 =n•3n,知Tn═3+2•32+3•33+…+n•3n,利用错位相减法能求出
=n•3n,知Tn═3+2•32+3•33+…+n•3n,利用错位相减法能求出 .不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,由此能求出实数λ的最大值.
.不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)•3n+1,由此能求出实数λ的最大值.点评:本题考查数列的通项公式的求法,求实数λ的最大值.综合性强,难度大,是高考的重点,易错点是不等式λ(an-2n)≤4Tn化为λ≤(2n-1)•3n+1.解题时要认真审题,仔细解答,注意极限的合理运用.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |