题目内容
已知曲线C1的极坐标方程为ρcos(θ- )=-1,曲线C2的极坐标方程为ρ=2
)=-1,曲线C2的极坐标方程为ρ=2 cos(θ-
cos(θ- ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
【答案】
(1) (2)
(2)
【解析】
试题分析:解:(Ⅰ) ,
,
即 ,可得
,可得 ,
,
故 的直角坐标方程为
的直角坐标方程为 . (5分)
. (5分)
(Ⅱ) 的直角坐标方程为
的直角坐标方程为 ,
,
由(Ⅰ)知曲线 是以
是以 为圆心的圆,且圆心到直线
为圆心的圆,且圆心到直线 的距离
的距离 ,
,
所以动点 到曲线
到曲线 的距离的最大值为
的距离的最大值为 . (10分)
. (10分)
考点:直线与圆的位置关系
点评:主要是考查了直线与圆的位置关系,以及点到直线的距离公式的运用,属于基础题。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
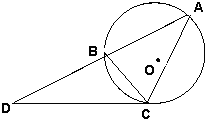 (1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,
(1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,