题目内容
下列说法:①向量 满足
满足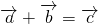 ,则
,则 可以是一个三角形的一条边长;②△ABC中,如果
可以是一个三角形的一条边长;②△ABC中,如果 ,那么△ABC是等腰三角形;③△ABC中,若
,那么△ABC是等腰三角形;③△ABC中,若 >0,则△ABC是锐角三角形;④△ABC中,若
>0,则△ABC是锐角三角形;④△ABC中,若 =0,△ABC是直角三角形.其中正确的个数是________.
=0,△ABC是直角三角形.其中正确的个数是________.
3个
分析:①根据向量加法的三角形法则即可得到结论是正确的;
②根据△ABC中, ,可得AB=BC,从而可知该命题是正确的;
,可得AB=BC,从而可知该命题是正确的;
③△ABC中,若 >0,根据向量数量积的定义,可知∠B是钝角,因此结论错误;
>0,根据向量数量积的定义,可知∠B是钝角,因此结论错误;
④△ABC中,若 =0,根据向量数量积的定义,可知∠B是直角,可知结论正确,从而得到答案.
=0,根据向量数量积的定义,可知∠B是直角,可知结论正确,从而得到答案.
解答:①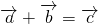 ,根据向量加法的三角形法则,即可知则
,根据向量加法的三角形法则,即可知则 可以是一个三角形边长;故①正确;
可以是一个三角形边长;故①正确;
②△ABC中, ,则AB=BC,∴△ABC是等腰三角形,故②正确;
,则AB=BC,∴△ABC是等腰三角形,故②正确;
③△ABC中,若 >0,则∠B是钝角,∴△ABC是锐角三角形;故③错;
>0,则∠B是钝角,∴△ABC是锐角三角形;故③错;
④△ABC中,若 =0,则∠B是直角,∴△ABC是直角三角形,故④正确;
=0,则∠B是直角,∴△ABC是直角三角形,故④正确;
因此正确的个数是3个
故答案为:3个.
点评:本题比较综合的考查了三角形和平面向量的相关性质,做为解析几何的基础知识点,平面向量在判断三角形形状,证明三角形的相关性质方面有较广的应用,特别是平面向量垂直的充要条件和平面向量夹角公式,一定要引起大家足够的重视,属中档题.
分析:①根据向量加法的三角形法则即可得到结论是正确的;
②根据△ABC中,
 ,可得AB=BC,从而可知该命题是正确的;
,可得AB=BC,从而可知该命题是正确的;③△ABC中,若
 >0,根据向量数量积的定义,可知∠B是钝角,因此结论错误;
>0,根据向量数量积的定义,可知∠B是钝角,因此结论错误;④△ABC中,若
 =0,根据向量数量积的定义,可知∠B是直角,可知结论正确,从而得到答案.
=0,根据向量数量积的定义,可知∠B是直角,可知结论正确,从而得到答案.解答:①
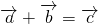 ,根据向量加法的三角形法则,即可知则
,根据向量加法的三角形法则,即可知则 可以是一个三角形边长;故①正确;
可以是一个三角形边长;故①正确;②△ABC中,
 ,则AB=BC,∴△ABC是等腰三角形,故②正确;
,则AB=BC,∴△ABC是等腰三角形,故②正确;③△ABC中,若
 >0,则∠B是钝角,∴△ABC是锐角三角形;故③错;
>0,则∠B是钝角,∴△ABC是锐角三角形;故③错;④△ABC中,若
 =0,则∠B是直角,∴△ABC是直角三角形,故④正确;
=0,则∠B是直角,∴△ABC是直角三角形,故④正确;因此正确的个数是3个
故答案为:3个.
点评:本题比较综合的考查了三角形和平面向量的相关性质,做为解析几何的基础知识点,平面向量在判断三角形形状,证明三角形的相关性质方面有较广的应用,特别是平面向量垂直的充要条件和平面向量夹角公式,一定要引起大家足够的重视,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设平面向量
=(x1,y1),
=(x2,y2),定义运算⊙:
⊙
=x1y2-y1x2.已知平面向量
,
,
,则下列说法错误的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| c |
A、(
| ||||||||||||||
B、存在非零向量a,b同时满足
| ||||||||||||||
C、(
| ||||||||||||||
D、|
|
 满足
满足 ,则
,则 可以是一个三角形的一条边长;②△ABC中,如果
可以是一个三角形的一条边长;②△ABC中,如果 ,那么△ABC是等腰三角形;③△ABC中,若
,那么△ABC是等腰三角形;③△ABC中,若 >0,则△ABC是锐角三角形;④△ABC中,若
>0,则△ABC是锐角三角形;④△ABC中,若 =0,△ABC是直角三角形.其中正确的个数是 .
=0,△ABC是直角三角形.其中正确的个数是 .