题目内容
已知双曲线
（a＞0，b＞0）的离心率e=2，过双曲线上一点M作直线MA，MB交双曲线于A，B两点，且斜率分别为k1，k2．若直线AB过原点，则k1•k2的值为
- A.2
- B.3
- C.
- D.
B
分析：设出M、N、P，表示出k1•k2，M、N、P代入双曲线方程并化简，代入双曲线的离心率乘积，求出k1•k2的值．
解答：因为过双曲线上一点M作直线MA，MB交双曲线于A，B两点，且斜率分别为k1，k2．若直线AB过原点，
所以A、B关于原点对称，
设M（p，q），N（-p，-q），P（s，t），
则有k1•k2=
=
，
，
，
两式相等得：
，
即
，=
，
k1•k2===
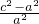=22-1=3．
故选B．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质，考查转化思想，化简得到 K1•K2是解题的关键．
分析：设出M、N、P，表示出k1•k2，M、N、P代入双曲线方程并化简，代入双曲线的离心率乘积，求出k1•k2的值．
解答：因为过双曲线上一点M作直线MA，MB交双曲线于A，B两点，且斜率分别为k1，k2．若直线AB过原点，
所以A、B关于原点对称，
设M（p，q），N（-p，-q），P（s，t），
则有k1•k2=
=，，，两式相等得：
，即
，=，k1•k2=
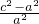===22-1=3．故选B．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质，考查转化思想，化简得到 K1•K2是解题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
-
=1(a＞0,b＞0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
(O为原点),则两条渐近线的夹角为( )
=1(a＞0,b＞0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
(O为原点),则两条渐近线的夹角为( )
（a＞0，b＞0）的左右焦点分别为F1、 F2 ,P 是双曲线上的一点，且P F1⊥P F2, 
的面积为2 ab,则双曲线的离心率 e=________．
（a>0,b>0）的两条渐近线均和圆C：x2+y2-6x+5=0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为（ ）
（B）
（C）
（D）