题目内容
矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的体积为
.
| 24 |
| 5 |
| 24 |
| 5 |
分析:先作BO⊥AC,可得BO⊥平面ADC;通过面积相等可得BO得长,在代入体积计算公式即可.
解答: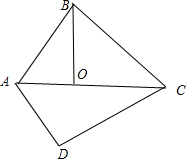 解:作BO⊥AC于O;
解:作BO⊥AC于O;
∵是直二面角B-AC-D
∴BO⊥平面ADC;
在△ABC,AB=4,BC=3⇒AC=5;
∵
BO•AC=
AB•BC⇒BO=
.
∴VB-ACD=
•BO•S△ADC
=
×
×
×3×4
=
.
故答案为:
.
 解:作BO⊥AC于O;
解:作BO⊥AC于O;∵是直二面角B-AC-D
∴BO⊥平面ADC;
在△ABC,AB=4,BC=3⇒AC=5;
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
∴VB-ACD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 12 |
| 5 |
| 1 |
| 2 |
=
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |
点评:本题主要考察与二面角有关的立体几何综合题.解决本题得关键在于根据面面垂直得到BO⊥平面ADC.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,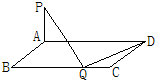 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于