题目内容
有以下四个命题：①两直线m，n与平面α所成的角相等的充要条件是m∥n；
②若p：?x∈R，sinx≤1，则￢P：?x∈R，sinx＞1；
③不等式10x＞x2在（0，+∞）上恒成立；
④设有四个函数
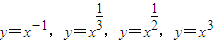，其中在R上是增函数的函数有3个．其中真命题的序号是 ．（漏填、多填或错填均不得分）
【答案】分析：①通过举特殊情形，m，n与平面α均平行，且相交时，判断错误
②根据特称命题的否定判断
③根据指数函数和幂函数的增长快慢判断
④根据幂函数的图象与性质判断
解答：解：①当两直线m，n与平面α均平行，且相交时，所成的角相等，均为0度，显然错误
②若p：?x∈R，sinx≤1，则￢P：?x∈R，sinx＞1 正确
③根据特称命题的否定判断，可知③正确
④根据幂函数的图象与性质，只有
R上是增函数
故答案为：②③
点评：本题考查命题的真假，用到了线面角、函数的图象与性质等知识．
②根据特称命题的否定判断
③根据指数函数和幂函数的增长快慢判断
④根据幂函数的图象与性质判断
解答：解：①当两直线m，n与平面α均平行，且相交时，所成的角相等，均为0度，显然错误
②若p：?x∈R，sinx≤1，则￢P：?x∈R，sinx＞1 正确
③根据特称命题的否定判断，可知③正确
④根据幂函数的图象与性质，只有
R上是增函数故答案为：②③
点评：本题考查命题的真假，用到了线面角、函数的图象与性质等知识．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目