题目内容
已知点集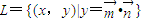 ,其中
,其中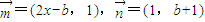 ,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,n∈N+.
,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,n∈N+.(1)求数列{an},{bn}的通项公式;
(2)若
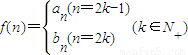 ,是否存在k∈N+使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.
,是否存在k∈N+使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.(3)求证:
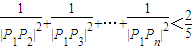 (n≥2,n∈N*).
(n≥2,n∈N*).
【答案】分析:(1)由y= 及
及 ,可得L:y=2x+1,从而得P1(0,1),则a1=0,b1=1,由等差数列通项公式可得an,代入y=2x-1可得bn;
,可得L:y=2x+1,从而得P1(0,1),则a1=0,b1=1,由等差数列通项公式可得an,代入y=2x-1可得bn;
(2)假设存在符合条件的k使命题成立,分k为偶数,k为奇数两种情况进行讨论,分别表示出f(k+11),f(k),根据方程f(k+11)=2f(k),可解得k;
(3)当n≥2时,Pn(n-1,2n-1),可得|P1Pn|= (n-1),则
(n-1),则 =
= ,对分母进行放缩后利用裂项相消法可进行化简,根据其范围可得结论;
,对分母进行放缩后利用裂项相消法可进行化简,根据其范围可得结论;
解答:解:(1)由 ,得y=2x+1,
,得y=2x+1,
∴L:y=2x+1,∴P1(0,1),则a1=0,b1=1,
∴an=n-1(n∈N+),bn=2n-1(n∈N+).
(2)假设存在符合条件的k使命题成立,
当k是偶数时,k+11是奇数,则f(k+11)=k+10,f(k)=2k-1,
由f(k+11)=2f(k),得k=4;
当k是奇数时,k+11是偶数,则f(k+11)=2k+21,f(k)=k-1,
由f(k+11)=2f(k),得k无解;
综上存在k=4,使得f(k+11)=2f(k);
证明:(3)当n≥2时,Pn(n-1,2n-1),
∴|P1Pn|= (n-1),(n≥2)
(n-1),(n≥2)
∴
 .
.
点评:本题考查数列与不等式、数列与向量的综合,考查学生综合运用知识分析解决问题的能力.
 及
及 ,可得L:y=2x+1,从而得P1(0,1),则a1=0,b1=1,由等差数列通项公式可得an,代入y=2x-1可得bn;
,可得L:y=2x+1,从而得P1(0,1),则a1=0,b1=1,由等差数列通项公式可得an,代入y=2x-1可得bn;(2)假设存在符合条件的k使命题成立,分k为偶数,k为奇数两种情况进行讨论,分别表示出f(k+11),f(k),根据方程f(k+11)=2f(k),可解得k;
(3)当n≥2时,Pn(n-1,2n-1),可得|P1Pn|=
 (n-1),则
(n-1),则 =
= ,对分母进行放缩后利用裂项相消法可进行化简,根据其范围可得结论;
,对分母进行放缩后利用裂项相消法可进行化简,根据其范围可得结论;解答:解:(1)由
 ,得y=2x+1,
,得y=2x+1,∴L:y=2x+1,∴P1(0,1),则a1=0,b1=1,
∴an=n-1(n∈N+),bn=2n-1(n∈N+).
(2)假设存在符合条件的k使命题成立,
当k是偶数时,k+11是奇数,则f(k+11)=k+10,f(k)=2k-1,
由f(k+11)=2f(k),得k=4;
当k是奇数时,k+11是偶数,则f(k+11)=2k+21,f(k)=k-1,
由f(k+11)=2f(k),得k无解;
综上存在k=4,使得f(k+11)=2f(k);
证明:(3)当n≥2时,Pn(n-1,2n-1),
∴|P1Pn|=
 (n-1),(n≥2)
(n-1),(n≥2)∴

 .
.点评:本题考查数列与不等式、数列与向量的综合,考查学生综合运用知识分析解决问题的能力.

练习册系列答案
相关题目
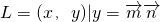 ,其中
,其中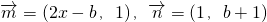 ,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,(n∈N+)
,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,(n∈N+)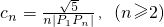 ,求
,求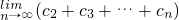
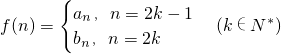 ,是否存在k∈N+,使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.
,是否存在k∈N+,使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.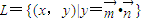 ,其中
,其中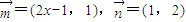 ,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.
,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.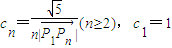 ,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.
,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.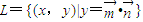 ,其中
,其中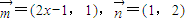 ,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.
,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.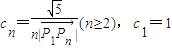 ,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.
,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.