��Ŀ����
ij��������һ��������Ԫ�������������������ͼ���ˮƽ�����ƣ������һЩ��Ʒ�����ݾ���֪�������Ʒ��P���ղ���x�������֮����������ϵ��P=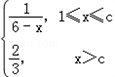 ������cΪС��6������������ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
������cΪС��6������������ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
��1���Խ���������������Ԫ��ÿ���ӯ����T����Ԫ����ʾΪ�ղ���x��������ĺ�����
��2�����ղ���Ϊ����ʱ���ɻ���������
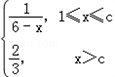 ������cΪС��6������������ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
������cΪС��6������������ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�������1���Խ���������������Ԫ��ÿ���ӯ����T����Ԫ����ʾΪ�ղ���x��������ĺ�����
��2�����ղ���Ϊ����ʱ���ɻ���������
�⣺��1����x��cʱ��P= ��
��
��T= x2��
x2�� x1=0
x1=0
��1��x��cʱ�� ��
��
�� =
=
���ϣ���ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��

��2���ɣ�1��֪����x��cʱ��ÿ���ӯ����Ϊ0
��1��x��cʱ��T= =15��2[��6��x��+
=15��2[��6��x��+ ]��15��12=3
]��15��12=3
���ҽ���x=3ʱȡ�Ⱥ�
���Ԣٵ�3��c��6ʱ��Tmax=3����ʱx=3
�ڵ�1��c��3ʱ����T'= =
= ֪
֪
����T= ��[1��3]�ϵ�����Tmax=
��[1��3]�ϵ�����Tmax= ����ʱx=c
����ʱx=c
���ϣ���3��c��6�����ղ���Ϊ3���ʱ���ɻ���������
��1��c��3�����ղ���Ϊc���ʱ���ɻ���������
 ��
����T=
 x2��
x2�� x1=0
x1=0��1��x��cʱ��
 ��
����
 =
=
���ϣ���ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��

��2���ɣ�1��֪����x��cʱ��ÿ���ӯ����Ϊ0
��1��x��cʱ��T=
 =15��2[��6��x��+
=15��2[��6��x��+ ]��15��12=3
]��15��12=3���ҽ���x=3ʱȡ�Ⱥ�
���Ԣٵ�3��c��6ʱ��Tmax=3����ʱx=3
�ڵ�1��c��3ʱ����T'=
 =
= ֪
֪����T=
 ��[1��3]�ϵ�����Tmax=
��[1��3]�ϵ�����Tmax= ����ʱx=c
����ʱx=c���ϣ���3��c��6�����ղ���Ϊ3���ʱ���ɻ���������
��1��c��3�����ղ���Ϊc���ʱ���ɻ���������

��ϰ��ϵ�д�
 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
�����Ŀ
 ��֪ÿ����l����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����l�����Ʒ������1��Ԫ��������=ӯ��һ����
��֪ÿ����l����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����l�����Ʒ������1��Ԫ��������=ӯ��һ���� ���ղ���
���ղ��� �������֮�������ϵ��
�������֮�������ϵ�� ������
������ ΪС��6������������ע����Ʒ��=��Ʒ��/����������
ΪС��6������������ע����Ʒ��=��Ʒ��/���������� ��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ��
��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ�� (��Ԫ����ʾΪ�ղ���
(��Ԫ����ʾΪ�ղ���