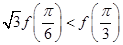题目内容
已知函数f(x)=(ax+1)ex.
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[-2,0]上的最小值.
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[-2,0]上的最小值.
(1)见解析
(2)当a>1时,f(x)在区间[-2,0]上的最小值为-a·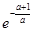 ;
;
当0<a≤1时,f(x)在区间[-2,0]上的最小值为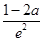 .
.
(2)当a>1时,f(x)在区间[-2,0]上的最小值为-a·
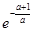 ;
;当0<a≤1时,f(x)在区间[-2,0]上的最小值为
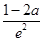 .
.解:依题意,函数的定义域为R,
f′(x)=(ax+1)′ex+(ax+1)(ex)′=ex(ax+a+1).
(1)①当a=0时,f′(x)=ex>0,
则f(x)的单调递增区间为(-∞,+∞);
②当a>0时,由f′(x)>0,解得x>- ,
,
由f′(x)<0,解得x<- ,
,
则f(x)的单调递增区间为(- ,+∞),
,+∞),
f(x)的单调递减区间为(-∞,- );
);
③当a<0时,由f′(x)>0,解得x<- ,
,
由f′(x)<0解得,x>- ,
,
则f(x)的单调递增区间为(-∞,- ),
),
f(x)的单调递减区间为(- ,+∞).
,+∞).
(2)①当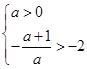 时,
时, )上是减函数,
)上是减函数,
在(- ,0)上是增函数,
,0)上是增函数,
则函数f(x)在区间[-2,0]上的最小值为f(- )=-a·
)=-a·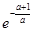 ;
;
②当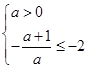 时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=
时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=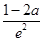 .
.
综上,当a>1时,f(x)在区间[-2,0]上的最小值为-a·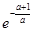 ;
;
当0<a≤1时,f(x)在区间[-2,0]上的最小值为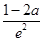 .
.
f′(x)=(ax+1)′ex+(ax+1)(ex)′=ex(ax+a+1).
(1)①当a=0时,f′(x)=ex>0,
则f(x)的单调递增区间为(-∞,+∞);
②当a>0时,由f′(x)>0,解得x>-
 ,
,由f′(x)<0,解得x<-
 ,
,则f(x)的单调递增区间为(-
 ,+∞),
,+∞),f(x)的单调递减区间为(-∞,-
 );
);③当a<0时,由f′(x)>0,解得x<-
 ,
,由f′(x)<0解得,x>-
 ,
,则f(x)的单调递增区间为(-∞,-
 ),
),f(x)的单调递减区间为(-
 ,+∞).
,+∞).(2)①当
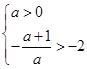 时,
时, )上是减函数,
)上是减函数,在(-
 ,0)上是增函数,
,0)上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-
 )=-a·
)=-a·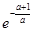 ;
;②当
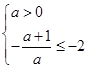 时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=
时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=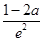 .
.综上,当a>1时,f(x)在区间[-2,0]上的最小值为-a·
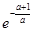 ;
;当0<a≤1时,f(x)在区间[-2,0]上的最小值为
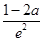 .
.
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,
, .若
.若
 的值;
的值; 的单调区间及极值.
的单调区间及极值.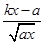 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).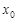 是函数
是函数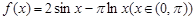 的零点,
的零点,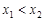 ,则:①
,则:①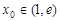 ;②
;②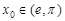 ;
;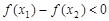 ;④
;④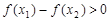 ,其中正确的命题是( )
,其中正确的命题是( )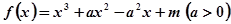
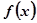 的单调增区间;
的单调增区间;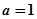 时,函数
时,函数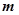 的取值范围.
的取值范围.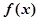 的导函数为
的导函数为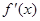 ,函数
,函数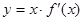 的图象的一部分如下图所示,则( )
的图象的一部分如下图所示,则( )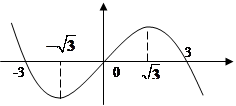
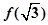 ,极小值为
,极小值为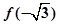
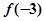 ,极小值为
,极小值为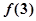
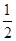 x2-alnx(a∈R).
x2-alnx(a∈R). 上的函数
上的函数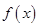 ,其导函数是
,其导函数是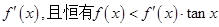 成立,则
成立,则