题目内容
已知正三棱锥的底面边长为6，斜高为3，则此三棱锥的体积为 ．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：画出图形，求出底面中心和底边中点的距离，然后求出底面三角形的CO，再求棱锥的高，即可求出正三棱锥的体积．
解答：
解：由题意画出图形，底面中心和底边中点的距离为：CO=
×
×6=
，
所以，棱锥的斜高为3，棱锥的高为：h=
=2
．
三棱锥的体积为：
Sh=
×
×62×2
=18．
故答案为：18．
解：由题意画出图形，底面中心和底边中点的距离为：CO=| 1 |
| 3 |
| ||
| 2 |
| 3 |
所以，棱锥的斜高为3，棱锥的高为：h=
32+(
|
| 3 |
三棱锥的体积为：
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
故答案为：18．
点评：本题考查棱锥的体积，考查计算能力，基本知识的考查．
练习册系列答案
相关题目
已知{an}是等差数列，且a2=-5，a5=a3+6，则a1=（ ）
| A、-2 | B、-7 | C、-8 | D、-9 |
为了调查教师对党的群众路线学习情况，教委拟采用分层抽样的方法从甲乙丙三所不同的中学抽取90名教师进行调查．已知甲乙丙校中分别有180，270，90名教师，则从C学校中应抽取的人数为（ ）
| A、10 | B、60 | C、15 | D、24 |
给出以下四个命题：
①若x，y∈N*，x+y是奇数，则x，y中一个是奇数一个是偶数；
②若-2≤x＜3，则（x+2）（x-3）≤0；
③若x=y=0，则x2+y2=0；
④若x2-3x+2=0，则x=1或x=2．
那么（ ）
①若x，y∈N*，x+y是奇数，则x，y中一个是奇数一个是偶数；
②若-2≤x＜3，则（x+2）（x-3）≤0；
③若x=y=0，则x2+y2=0；
④若x2-3x+2=0，则x=1或x=2．
那么（ ）
| A、①为假命题 |
| B、②的否命题为真 |
| C、③的逆否命题为假 |
| D、④的逆命题为真 |
已知函数f（x）=（2x-x2）ex，则（ ）
A、f(
| ||
B、f(
| ||
C、f(-
| ||
| D、f（x）没有最大值也没有最小值 |
下列说法错误的是（ ）
| A、已知命题p为“?x∈[0，+∞），（log32）x≤1”，则￢p是真命题 |
| B、若p∨q为假命题，则p、q均为假命题 |
| C、x＞2是x＞1充分不必要条件 |
| D、“全等三角形的面积相等”的否命题是假命题 |
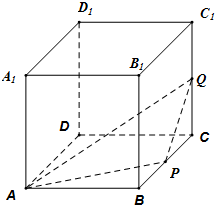正方体ABCD-A1B1C1D1为棱长为1，动点P，Q分别在棱BC，CC1上，过点A，P，Q的平面截该正方体所得的截面记为S，设BP=x，CQ=y，其中x，y∈[0，1]，下列命题正确的是