题目内容
已知 图象过点
图象过点 ,且在
,且在 处的切线方程是
处的切线方程是 .
.
(1)求 的解析式;
的解析式;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(1)
(2)当 时,
时, ;当
;当 时,
时,
【解析】
试题分析:(1)由于过函数图象过点把点的坐标代入,可求得c利用相切列关于a,b的方程.
(2)对解析式求导,然后列表,判断单调性,可求导最值.
试题解析:【解析】
(1) , 1分
, 1分
 ,∴
,∴ ,∴
,∴ 3分
3分
又∵切点为 ,∴
,∴ 5分
5分
联立可得 6分
6分
∴ 7分
7分
(2)
 , 8分
, 8分
令 ,
,
令 或
或 ,
,
令 , 10分
, 10分
|
|
|
|
| 2 |
| 3 |
| + | 0 | - | 0 | + | ||
|
| ↗ | 5 | ↘ |
| ↗ |
|
由上表知,在区间 上,当
上,当 时,
时,
当 时,
时, 14分
14分
考点:利用导数判断函数的单调性以及最值.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目











 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是( )
的值是( ) 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( ) B.
B. C.
C. D.
D.
 的零点个数为( )
的零点个数为( ) ( )
( ) B、
B、 C、
C、 D、
D、
 ,
, ,
, ,则
,则 与
与 夹角的度数为 .
夹角的度数为 . 是( )
是( )
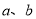 分别是方程
分别是方程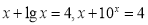 的解,
的解, 则关于
则关于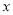 的方程
的方程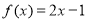 的解的个数是( )
的解的个数是( ) ,
, ,则
,则 为邻边的平行四边形的面积为 .
为邻边的平行四边形的面积为 .