题目内容
如图，P是椭圆
上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上一点，且
．则|OM|的取值范围 ．
【答案】分析：延长F2M交PF1于点N，由题意可知△PNF2为等腰三角形，得OM是△PF1F2的中位线．利用三角形中位线定理和椭圆的定义，算出|OM|=a-|PF2|，再由椭圆的焦半径|PF2|的取值范围加以计算，即可得到|OM|的取值范围．
解答：解：∵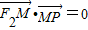
，∴
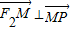
延长F2M交PF1于点N，可知△PNF2为等腰三角形，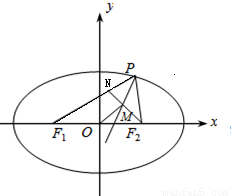
且M为F2M的中点，可得OM是△PF1F2的中位线
∴|OM|=
|NF1|=
（|PF1|-|PN|）
=
（|PF1|-|PF2|）=
（2a-2|PF2|）=a-|PF2|
∵a-c＜|PF2|＜a+c
∴0＜|OM|＜c=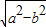
=3
∴|OM|的取值范围是（0，3）
故答案为：（0，3）
点评：本题给出椭圆焦点三角形角平分线的垂线，求垂足到椭圆中心距离的范围．着重考查了椭圆的定义与简单几何性质、等腰三角形的判定与性质和三角形中位线定理等知识，属于中档题．
解答：解：∵
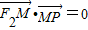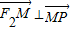
，∴延长F2M交PF1于点N，可知△PNF2为等腰三角形，
且M为F2M的中点，可得OM是△PF1F2的中位线
∴|OM|=
|NF1|=（|PF1|-|PN|）=
（|PF1|-|PF2|）=（2a-2|PF2|）=a-|PF2|∵a-c＜|PF2|＜a+c
∴0＜|OM|＜c=
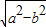=3∴|OM|的取值范围是（0，3）
故答案为：（0，3）
点评：本题给出椭圆焦点三角形角平分线的垂线，求垂足到椭圆中心距离的范围．着重考查了椭圆的定义与简单几何性质、等腰三角形的判定与性质和三角形中位线定理等知识，属于中档题．
练习册系列答案
相关题目
．如图，P是双曲线
上的动点，F1、
F2是双曲线的焦点，M是
的平分线上一点，且
某同学用以下方法研究|OM|：延长F2M交PF1于点N，可知
为
等腰三角形，且M为F2M的中点，得
|
上的动点，F1、F2是椭圆的焦点，M是的平分线上一点，且
.则|OM|的取值范围是
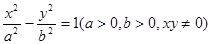上的动点，
、
是双曲线的左右焦点，
是
的平分线上一点，且
某同学用以下方法研究
：延长
交
于点
，可知
为等腰三角形，且M为
的中点，得
类似地：P是椭圆
上的动点，
，则
上的动点，F1、F2是双曲线的焦点，M是
的平分线上一点，且
某同学用以下方法研究|OM|：延长
交
于点N，可知
为等腰三角形，且M为
的中点，得
类似地：P是椭圆
上的动点，F1、F2是椭圆的焦点，M是
，则|OM|的取值范围是
．
上的动点，F1、F2是双曲线的焦点，M是∠F1PF2的平分线上一点，且
．某同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2M的中点，得
．类似地：P是椭圆
上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上一点，且
．则|OM|的取值范围是 ．