题目内容

若集合M={y|y= $数学公式$ }，P={y|y= $数学公式$ }，那么M∩P=________．

（0，+∞）
分析：集合M和集合P的公共元素构成集合M∩P，由此利用集合M={y|y= $\text{[math]}$ }={y|y＞0}，P={y|y= $\text{[math]}$ }={y|y≥0}，能求出M∩P．
解答：∵集合M={y|y= $\text{[math]}$ }={y|y＞0}，
P={y|y= $\text{[math]}$ }={y|y≥0}，
∴M∩P=（0，+∞）．
故答案为：（0，+∞）．
点评：本题考查集合的交集及其运算，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．

练习册系列答案

寒假拔高15天系列答案

衡水假期伴学寒假作业系列答案

欢乐假期寒假作业系列答案

黄冈小状元寒假作业龙门书局系列答案

黄冈状元成才路寒假作业系列答案

激活思维寒假作业系列答案

品至教育假期复习计划期末寒假衔接系列答案

假期园地寒假系列答案

假期生活寒假花山文艺出版社系列答案

南方凤凰台假期之友寒假作业江苏凤凰教育出版社系列答案

相关题目

若集合M={y|y=2-x}，P={y|y=

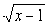}，则M∩P等于（　　）

若集合M={y|y=2^x}，P={y|y=}，则M∩P等于（）

A．{y|y>1} B．{y|y≥1}

C．{y|y>0} D．{y|y≥0}

若集合M={y|y=2^x，x∈R}，

，则M∩P=（）
A．{y|y＞1}
B．{y|y≥1}
C．{y|y＞0}
D．{y|y≥0}

若集合M={y|y=2^x，x∈R}，

，则M∩P=（）
A．{y|y＞1}
B．{y|y≥1}
C．{y|y＞0}
D．{y|y≥0}

若集合M={y|y=2^x，x∈R}，

，则M∩P=（）
A．{y|y＞1}
B．{y|y≥1}
C．{y|y＞0}
D．{y|y≥0}